- 真题试卷
- 模拟试卷
- 预测试卷
9. 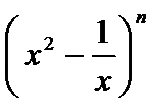
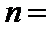
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.若数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
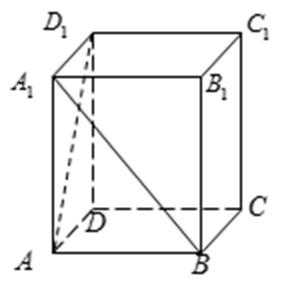
7.如图,正四棱柱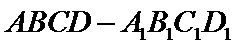
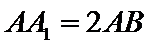
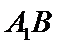
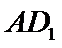
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.复数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.从5名候选同学中选出3名,分别保送北大小语种(每个语种各一名同学):俄罗斯语.阿拉伯语与希伯莱语,其中甲.乙二人不愿学希伯莱语,则不同的选法共有( )种。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.在






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若不等式


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.为了了解学生遵守《中华人民共和国交通安全法》的情况,调查部门在某学校进行了如下的随机调查:向被调查者提出两个问题:
(1)你的学号是奇数吗?
(2)在过路口的时候你是否闯过红灯?
要求被调查者背对调查人抛掷一枚硬币,如果出现正面,就回答第(1)个问题;否则就回答第(2)个问题。被调查者不必告诉调查人员自己回答的是哪一个问题,只需要回答“是”或“不是”,因为只有被调查本人知道回答了哪个问题,所以都如实做了回答。如果被调查的600人(学号从1到600)中有180人回答了“是”,由此可以估计在这600人中闯过红灯的人数是( )。
正确答案
60
解析
解析已在路上飞奔,马上就到!
知识点
1.方程
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知农民收入由工资性收入和其他收入两部分构成.2005年某地区农民人均收入为3150元(其中工资性收入为1800元,其他收入为1350元),预计该地区自2006年起的5年内,农民的工资性收入将以6 %的年增长率增长,其他收入每年增加160元。根据以上数据,2010年该地区农民人均收入介于 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.设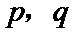
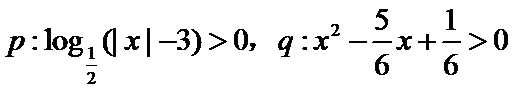
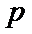
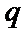
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知向量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知



正确答案
设
则
解得:





解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数


正确答案








解析
解析已在路上飞奔,马上就到!
知识点
21.已知公比为



(1)求数列


(2)对给定的




(3)设



①求


②求正整数

正确答案
(1)依题意可知,
(2)由(1)知,






(3) 



①
由

计算可得
因为当



②

当





解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数
(1)求
(2)请讨论它的单调性,并给予证明。
正确答案
(1)

即


经验证当

(2)先研究
得

由于

解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数



(1)若函数

(2)若当




(3)若当




正确答案
(1) 

(2)当



当

当



当




(3)当


易证函数

此时
若函数



显然当


所以
解析
解析已在路上飞奔,马上就到!
知识点
20.某段城铁线路上依次有A.B.C三站,AB=5km,BC=3km,在列车运行时刻表上,规定列车8时整从A站发车,8时07分到达B站并停车1分钟,8时12分到达C站,在实际运行中,假设列车从A站正点发车,在B站停留1分钟,并在行驶时以同一速度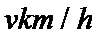
(1)分别写出列车在B.C两站的运行误差;(用含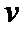
(2)若要求列车在B,C两站的运行误差之和不超过2分钟,求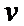
正确答案
(1)列车在B,C两站的运行误差(单位:分钟)分别是: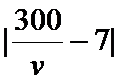
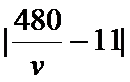
(2)由于列车在B,C两站的运行误差之和不超过2分钟,
所以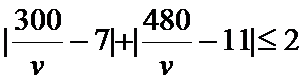
①当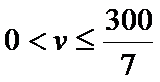
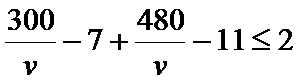
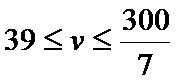
②当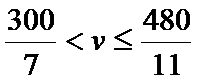
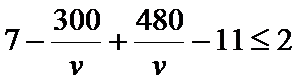
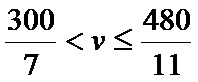
③当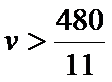
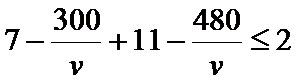

综上所述,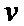
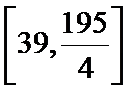
解析
解析已在路上飞奔,马上就到!