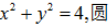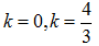- 真题试卷
- 模拟试卷
- 预测试卷
2.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.tanα=3x,tanβ=3–x,若α–β=
正确答案
0.5
解析
解析已在路上飞奔,马上就到!
知识点
7.直线l经过抛物线y2=4(x–1)的焦点,且与准线的夹角为30o,则l的方程为____.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.{a,b}
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知:f(x)=x2–4x+8,x∈[1,a]的最大值为f(a),则a∈_______.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.曲线

正确答案
(1,0)
解析
解析已在路上飞奔,马上就到!
知识点
8.△ABC中,AB=2a,BC=a,则∠A最大值为__________.
正确答案
30°
解析
解析已在路上飞奔,马上就到!
知识点
1. f(x)=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.z=1–2i,则
正确答案
-1+3i
解析
解析已在路上飞奔,马上就到!
知识点
10.平面α内∠AOB=90o,P
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.命题:三角形中,顶点与对边中点连线所得三线段交于一点,且分线段长度比为2:1,类比可得四面体中,顶点与所对面的_________连线所得四线段交于一点,且分线段比为_________.
正确答案
重心;3:1
解析
解析已在路上飞奔,马上就到!
知识点
11.已知曲线C:x2+(k–1)y2–3ky+2k=0 (k≠2). 给出下列命题:
(1)k=1,C是抛物线;
(2)1<k<2,C是焦点在y轴上椭圆;
(3)k>2,C是焦点在x轴上椭圆;
(4)k<1,k≠0,C是双曲线.
其中真命题序号是_______________.
正确答案
(1)(2)
解析
解析已在路上飞奔,马上就到!
知识点
14.已知:P(t,m)为y=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.若{an}的前n项和Sn=1+pan (p≠0,p≠1),则{an}是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.正方体ABCD-A1B1C1D1中,P是面AA1B1B上点,P到平面A1B1C1D1距离是P到BC距离的2倍,则P轨迹所在曲线是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.f(x)=x的点称为函数f(x)的不动点,设f(x)、g(x)都有不动点,则下列陈述正确的是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.某公司用300万元买回客船一艘,投入营运后,每月需开支燃油费、维修费、员工工资. 已知每月燃油费7000元,第n个月的维修费和工资支出为600(n–1)+3000元,如果把购船费和所有支出费用平摊到的每一个月,叫做每月平均消耗,当平均消耗最低时,营运成本最低.
(1)设月平均消耗y,写出y与n(月)的函数关系;
(2)投入营运几个月时,营运成本最低?
(3)若第一年纯收入50万,以后每年纯收入按5%递减,则多少年后可收回成本?
正确答案
(1)
(2)n=100
(3) 7年
解析
解析已在路上飞奔,马上就到!
知识点
18.在棱长为1的正方体ABCDA1B1C1D1中,E是A1B1中点.
(1)求过A、E、C1的截面面积;
(2)B到截面距离.
正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
17.已知:a>1. 解关于x的不等式(x+a)(a–
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列{xn}、{yn},xn+1=

(1){yn}是否为等差数列?说明理由;
(2)Sn是{yn}前n项和,Tn是

正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
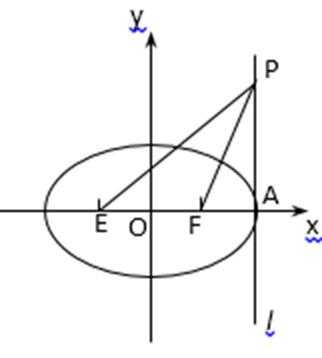
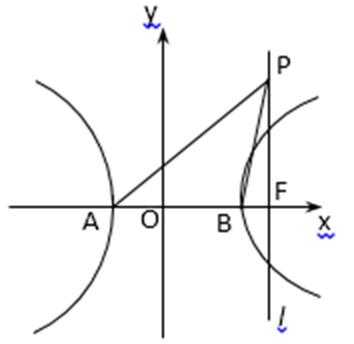
22.(1)A(–2,0)、B(2,0),M满足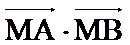
(2)若(1)中的轨迹按向量(1,–1)平移后恰与x+ky–3=0相切,求k.
(3)如图,l过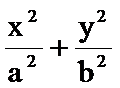
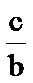
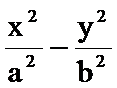
正确答案
(1)
(2)
(3)
解析
解析已在路上飞奔,马上就到!
知识点
21.已知△ABC三个内角满足A、B、C成等差,设x=cos

(1)求f(x)解析式及定义域;
(2)讨论函数单调性,并证明;
(3)求f(x)值域.
正确答案
(1)
(3)
解析
解析已在路上飞奔,马上就到!