- 真题试卷
- 模拟试卷
- 预测试卷
3.命题“
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.函数f(x)=
正确答案
(0,3]
解析
解析已在路上飞奔,马上就到!
知识点
5.在各项均为正数的等比数列{an}中,已知a1+ a2+ a3 =2, a3+ a4+ a5 =8,则a4+ a5+ a6 =( )
正确答案
16
解析
解析已在路上飞奔,马上就到!
知识点
10.已知f(x)=3sin(2x-
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设集合A={x|-
正确答案
{x|-1≤x<2}
解析
解析已在路上飞奔,马上就到!
知识点
2.复数i2(1-2i)的实部是( )
正确答案
(-1)
解析
解析已在路上飞奔,马上就到!
知识点
6.已知向量a,b满足|a|=1,|b|=2,a与b的夹角为60°,向量c=2a+b。则向量c的模为( )
正确答案
2
解析
|c|2=(2a+b)2=4a2+4a·b+b2=4+4×1×2×cos60°+4=12,即|c|=2
知识点
7.在平面直角坐标系xOy中,已知y=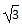
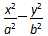
正确答案
2
解析
由题意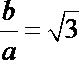
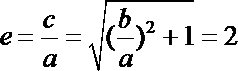
知识点
8.已知直线l⊥平面α,直线m
①若α∥β,则l⊥m;
②若α⊥β,则l∥m;
③若l∥m,则α⊥β;
④若l⊥m,则α∥β。
其中正确命题的序号是( )
正确答案
①③
解析
解析已在路上飞奔,马上就到!
知识点
9.若以连续掷两次骰子分别得到的点数m、n作为点P的横、纵坐标,则点P在直线x+y = 5下方的概率为( )
正确答案
解析
点P在直线x+y = 5下方的情况有(1,1),(1,2),(1,3),(2,1),(2,2),(3,1)六种可能,故其概率为
知识点
11.已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2+2x,若f(2-a2)>f(a),则实数a的取值范围是( )
正确答案
(-2,1)
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数f(x)= |lg(x-1)| 若a≠b,f(a)= f(b) ,则a+2b的取值范围是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 定义在R上的函数f(x)满足f(x)+f(x+5)=16,当x∈(-1,4]时,f(x)=x2-2x,则函数f(x)在[0,2013]上的零点个数是( )
正确答案
604
解析
由
则
所以
在一个周期


在
故
由于区间
又
故


知识点
14.已知函数f(x)=
正确答案
解析


则
原题等价为:对于

(1)当
(2)当



(3)当



综上,实数k的取值范围为
知识点
15.已知向量a=(2cosx , 2sinx) ,b=(

(1) f(x)的最小正周期和单调递增区间;
(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.如图,四边形ABCD为平行四边形,四边形ADEF是正方形,且BD⊥平面CDE,H是BE的中点,G是AE,DF的交点。
(1)求证:GH//平面CDE;
(2)求证:面ADEF⊥面ABCD。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知椭圆C:


(1)求椭圆C的方程;
(2)过原点且斜率为的直线l,与椭圆交于E,F点,试判断∠EF2F是锐角、直角还是钝角,并写出理由;
(3)P是椭圆上异于A1,A2的任一点,直线PA1,PA2,分别交
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知等差数列{an}中,首项a1=1,公差d为整数,且满足a1+3<a3, a2+5> a4,数列{bn}满足bn =
(1)求数列{an}的通项公式;
(2)若S2为S1,Sm (m∈N*)的等比中项,求正整数m的值。
(3)对任意正整数k,将等差数列{an}中落入区间(2k,22k)内项的个数记为ck,求数列{cn}的前n项和Tn
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,某自来水公司要在公路两侧铺设水管,公路为东西方向,在路北侧沿直线铺设线路l1,在路南侧沿直线铺设线路l2,现要在矩形区域ABCD内沿直线将l1与l2接通。已知AB = 60m,BC = 80m,公路两侧铺设水管的费用为每米1万元,穿过公路的EF部分铺设水管的费用为每米2万元,设∠EFB=
(1)求W关于α的函数关系式;
(2)求W的最小值及相应的角α。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数f(x)=a|x|+
(1)若a>1,且关于x的方程f(x)=m有两个不同的正数解,求实数m的取值范围;
(2)设函数g(x)= f(-x),x∈[-2,+∞),
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.口袋中有n(n∈N*)个白球,3个红球.依次从口袋中任取一球,如果取到红球,那么继续取球,且取出的红球不放回;如果取到白球,就停止取球.记取球的次数为X, 若P(X=2)=
求:
(1)n的值;
(2)X的概率分布与数学期望。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.设P1,P2,…,Pj为集合P={1,2,…,i}的子集,其中i,j为正整数.记aij为满足P1∩P2∩…∩Pj=
(1)求a22的值;
(2)求aij的表达式。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.【选做题】在下面A,B,C,D四个小题中只能选做两题。
A.选修4-1:几何证明选讲
如图,设AB为

求证:
(1)l是
(2)PB平分
B.选修4-2:矩阵与变
已知矩阵
(1)求矩阵MN;
(2)若点P在矩阵MN对应的变换作用下得到Q(0,1),求点P的坐标。
C.选修4-4:坐标系与参数方程
在直角坐标系xoy中,曲线C的参数方程为


D.选修4-5:不等式选讲
设


正确答案
A.
B.
C.
D.
解析
解析已在路上飞奔,马上就到!






























