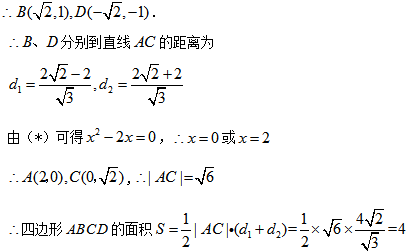- 真题试卷
- 模拟试卷
- 预测试卷
1. 已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 复数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 设



正确答案
充分不必要
解析
解析已在路上飞奔,马上就到!
知识点
4. 执行如图所示的算法流程图,则最后输出的
正确答案
31
解析
解析已在路上飞奔,马上就到!
知识点
6. 从集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 在平面直角坐标系





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 已知数列





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 已知正四棱锥的底面边长是

正确答案
12
解析
解析已在路上飞奔,马上就到!
知识点
7. 在




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 设函数








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 已知椭圆







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 一条宽为













(1) 如图①,已知村庄













正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 在



(1)当



(2)当

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 如图,在四棱锥







(1)求证:

(2)若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
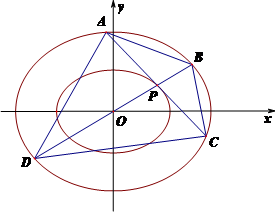
17. 已知曲线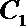
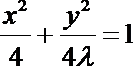
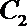
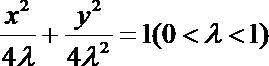
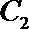
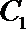
(1) 求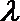
(2) 若曲线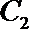
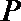
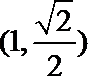
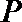
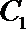
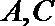
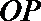
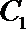
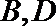
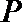
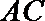
① 求直线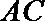
② 求四边形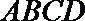
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知无穷数列









(1)当

(2)若

(3)判断是否存在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知函数
(1)若

(2)求证:当

(3)若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知直线的参数方程



(1)将直线的参数方程化为普通方程,圆
(2)求圆

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
24. 已知常数

(1)讨论

(2)若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22. 如图,正方形







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23. 如图,直三棱柱






(1)若






正确答案
解析
解析已在路上飞奔,马上就到!