- 真题试卷
- 模拟试卷
- 预测试卷
7.已知等比数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.如图,某几何体三视图如图所示,,其中侧(左)视图由半圆与两线段组成,则该几何体的体积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.下列函数中,在其定义域内既是奇函数又是减函数的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.随机抽取某产品


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知△ABC为等边三角形,





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.下面是关于复数



其中的真命题为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.为了解一片速生林的生长情况,随机测量了其中100株树木的底部周长(单位:cm).根据所得数据画出了样本的频率分布直方图(如下),那么在这100株树木中,底部周长小于110cm的株数是_______.
正确答案
70
解析
解析已在路上飞奔,马上就到!
知识点
11.将函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.计算:

正确答案
-20
解析
解析已在路上飞奔,马上就到!
知识点
选做题(14 - 15题,只能从中选做一题)
14.(坐标系与参数方程选做题)
在极坐标系中,曲线

15.(几何证明选讲选做题)
如图,








正确答案
14. 2
15. 3
解析
解析已在路上飞奔,马上就到!
知识点
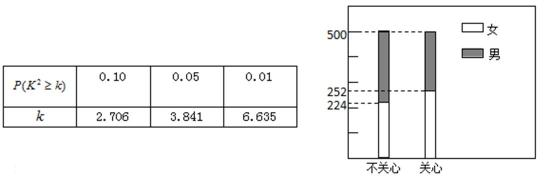
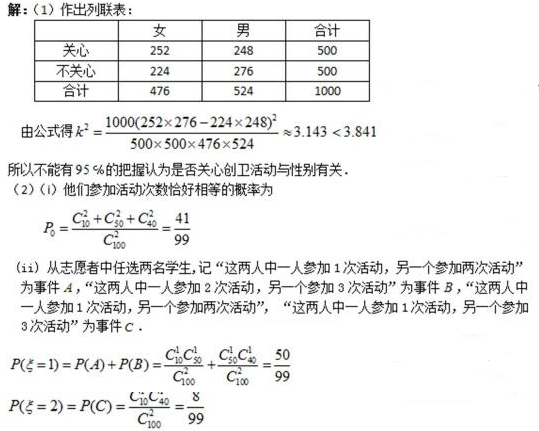
16.(某中学号召本校学生在本学期参加市创办卫生城的相关活动,学校团委对该校学生是否关心创卫活动用简单抽样方法调查了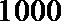
(1)完成列联表,并判断能否有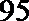
(参考数据与公式: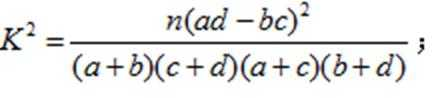
(2)已知校团委有青年志愿者100名,他们已参加活动的情况记录如下:
(i)从志愿者中任选两名学生,求他们参加活动次数恰好相等的概率;
(ii)从志愿者中任选两名学生,用
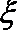

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,在路边安装路灯,灯柱与地面垂直,灯杆







(1)求灯柱的高

(2)若灯杆





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.(已知



(I)求
(II)当


(III)若存在属于区间




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,三棱锥








(1)证明:

(2)求直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知动点





(1)求

(2)点





(i)证明:
(ii)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.对数列








(1)已知数列



(2)若数列



(3)对(2)中数列




正确答案
解析
解析已在路上飞奔,马上就到!