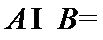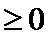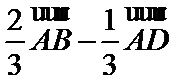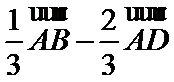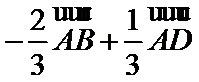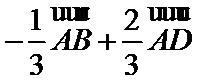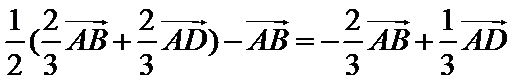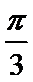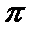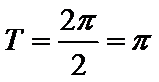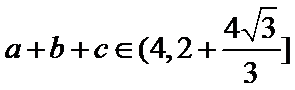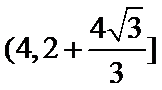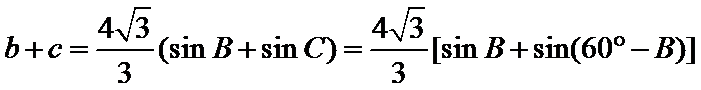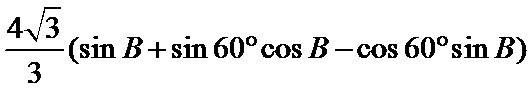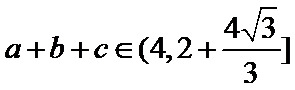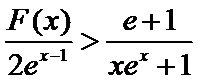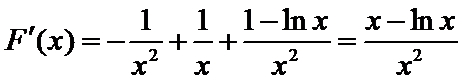- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合A={x|-2015≤x<2016},B={x|x|
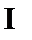
正确答案
解析
∵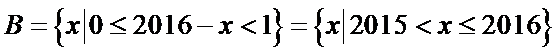

故A选项不正确,C选项不正确,D选项不正确,所以选B选项。
考查方向
解题思路
先解出集合B再进行A
易错点
易忽视2016-x
知识点
3.已知复数z满足(2+i)z =l+2i+3i2 +4i3(i为虚数单位),则z的共轭复数是( )
正确答案
解析
由
得


故A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
解题思路
先对等式右边化简再求出Z,最后写出
易错点
对
知识点
4.“C=5”是“点(2,1)到直线3x+4y十C=0的距离为3”的( )
正确答案
解析
由题意知点







考查方向
解题思路
先求出点(2,1)到直线3x+4y十C=0的距离为3的充要条件的C的值为

易错点
采用代入验证出错。
知识点
6.过双曲线

正确答案
解析
由题意,得




考查方向
解题思路
根据题意求出A,B两点的坐标,由△OAB的面积为
故A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
对△OAB的面积的转化较繁琐而出错。
知识点
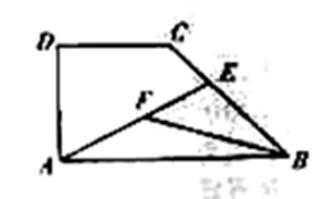
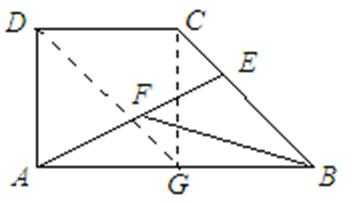
8.如图,在直角梯形ABCD中.AB=2AD=2DC,E为BC边上一点,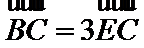
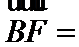
正确答案
解析
取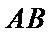
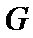
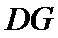
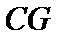
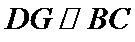
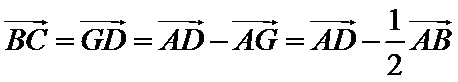
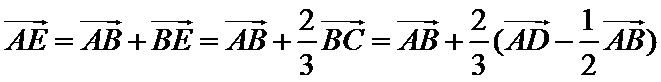
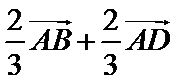
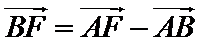
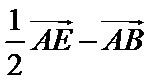
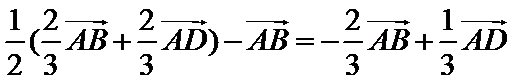
考查方向
解题思路
取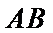
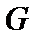
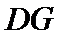
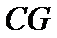
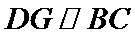
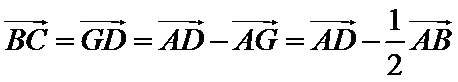
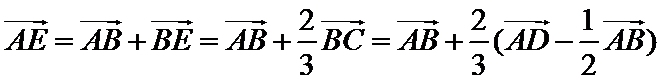
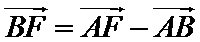
故A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
向量间的转化易出错
知识点
10. 已知(
正确答案
解析








故A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
解题思路
含x2与x3的项的系数,再根据绝对值之比为1:6,算得
易错点
确定项的系数时计算易出错。
知识点
2.函数f(x)= 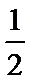
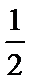
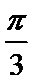
正确答案
解析
因为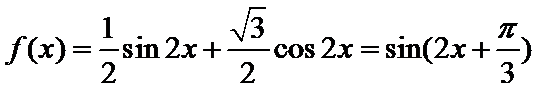
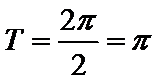
故A选项不正确,C选项不正确,D选项不正确,所以选B选项。
考查方向
解题思路
先化简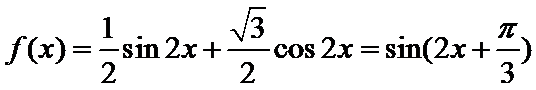
故A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
对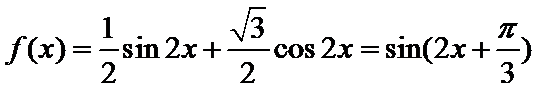
知识点
5.已知Sn为等差数列{an}的前n项和,若S3+S7= 37,则
正确答案
解析
由




故A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
解题思路
根据等差数列的性质求出
故A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
找不到已知和所求间的内在联系出错。
知识点
7.菜市中心购物商场在“双l1”开展的“买三免一”促销 活动异常火爆,对当日8时至22时的销售额进行统计,以组距为2小时的频率分布直方图如图所示.已知12:00时至16:00时的销售额为90万元,则10时至12时的销售额为( )
正确答案
解析
该商场11月11日8时至22时的总销售额为

故A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
解题思路
根据图像算出总销售额,再根据比例计算10时至12时的销售额。
故A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
计算总销售额易出错。
知识点
9.运行如图所示的程序,若输入x的值为256,则输出的y值是( )
正确答案
解析
根据程序框图及条件可知




故A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
解题思路
先将256代入计算得到新的x的值再进入判断框,直到算得
故A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
最后一步算y值时易算错。
知识点
11.如图ABCD -A1B1C1D1是边长为1的正方体,S- ABCD是高为l的正四棱锥,若点S,A1,B1,Cl,D1在同一个球面上,则该球的表面积为( )
正确答案
解析
按如图所示作辅助线,









故A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
解题思路
根据题意作图,找出球心位置,并设
故A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
球心的位置确定
知识点
12.在数列{an}中,a1=3, an=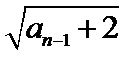
正确答案
解析
由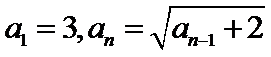
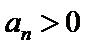
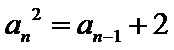
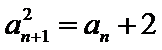
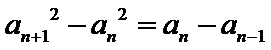
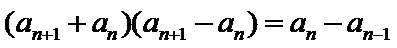
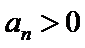
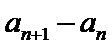
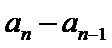
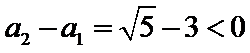
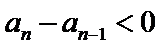
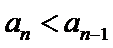
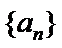
考查方向
解题思路
先对an=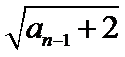
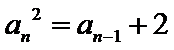
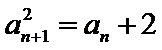
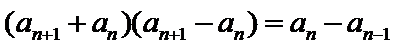
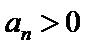
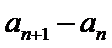
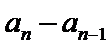
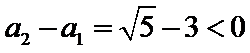
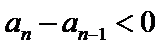
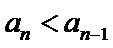
故B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
转化条件an=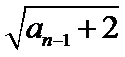
知识点
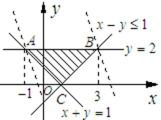
15.设x,y满足不等式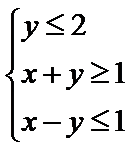
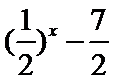
正确答案
解析
作出满足不等式的平面区域,如图所示,当直线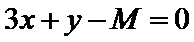
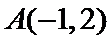
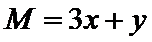
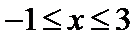
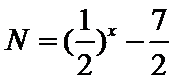
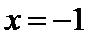
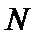
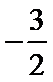

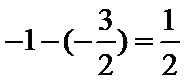
考查方向
解题思路
先作出可行域,再分别求出M,N的最值并确定取得最值的x的值是否相同。
易错点
当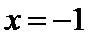
知识点
13.已知函数f(x)=(9x+1)·9kx(k∈R)为偶函数,则实数k的值为 .
正确答案
解析
由题意知






考查方向
解题思路
由于函数为偶函数,所以有



易错点
对偶函数的定义理解不清导致出错。
知识点
14. 已知直线l:y=kx+t号圆:x2 +(y+l)2 =1相切且与抛物线C:x2 =4y交于不同的两点M,N,则实数t的取值范围是____.
正确答案
解析
因为直线与圆相切





考查方向
解题思路
先利用直线与圆相切找到k与t之间的关系,再通过直线与抛物线有两个不同的交点求出t的取值范围。
易错点
直线中有两个变量,如何把k转化或者求出。
知识点
16.已知函数f(x)= cos2x +asinx在区间(0,n
则实数a的值为____ .
正确答案
解析
由





























考查方向
解题思路
先把函数的零点问题转化为方程的根的问题,即


易错点

知识点
在△ABC中,已知a,b, c分别是角A,B,C的对边,且满足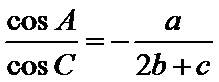
17.求角A的大小;
18.若a=2,求△ABC的周长的取值范围.
正确答案
(1)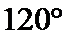
解析
(1)由正弦定理,得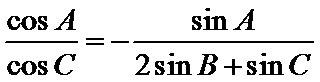
∴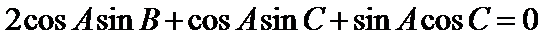
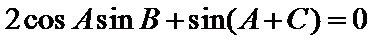
∵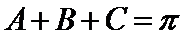
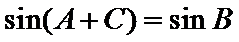
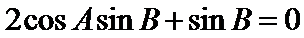
∵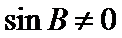
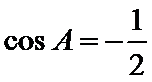
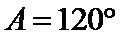
考查方向
解题思路
(1)利用已知条件和正弦定理求出角A(2)利用(1)中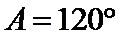
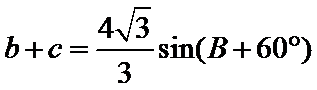
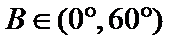
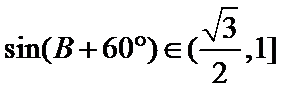
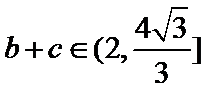
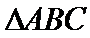
易错点
通过正弦定理表示三边即周长,易忽视角的范围出错。
正确答案
(2)
解析
(2)由正弦定理,得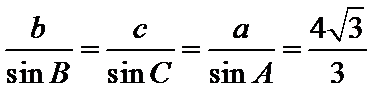
∴
=
=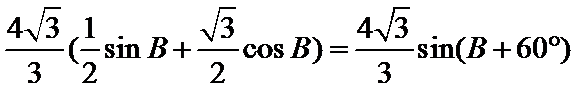
∵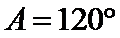
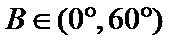
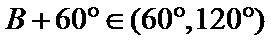
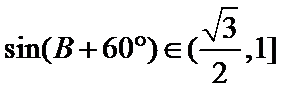
∴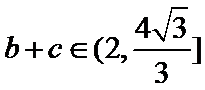
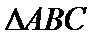
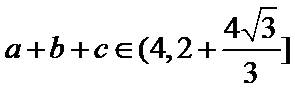
考查方向
解题思路
(1)利用已知条件和正弦定理求出角A(2)利用(1)中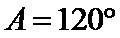
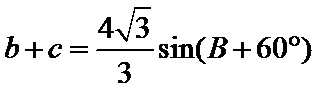
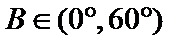
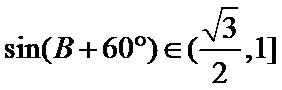
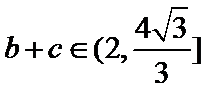
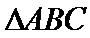
易错点
通过正弦定理表示三边即周长,易忽视角的范围出错。
新生儿Apgar评分,即阿氏评分是对新生儿出生后总体状况的一个评估,主要从呼吸、
心率、反射、肤色、肌张力这几个方面评分,满10分者为正常新生儿,评分7分以下的新
生儿考虑患有轻度窒息,评分在4分以下考虑患有重度窒息,大部分新生儿的评分多在7-10
分之间,某市级医院妇产科对1月份出生的新生儿随机制取了16名,以下表格记录了他们
的评分情况.
19.现从16名新生儿中随机抽取3名,求至多有1名评分不低于9分的概率:
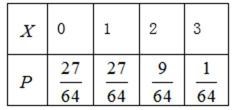
20.以这16名新生儿数据来估计本年度的总体数据,若从本市本年度新生儿中任选3名, 记X表示抽到评分不低于9分的新生儿数,求X的分布列及数学期望.
正确答案
(1)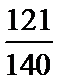
解析
(1)设
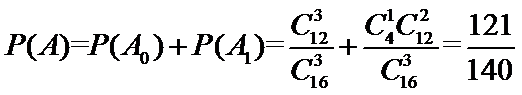
考查方向
解题思路
(1)先表示所求事件再计算其概率(2)写出X的所有可能取值并求出相应概率,列出分布列和计算数学期望。
易错点
所求事件的表示及概率的计算。
正确答案
(2)
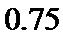
解析
(2)由表格数据知,从本本市年度新生儿中任选1名评分不低于9分的概率为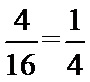
则由题意知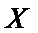
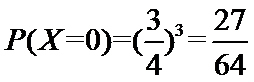
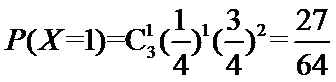

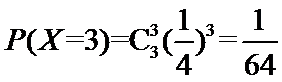
所以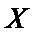
由表格得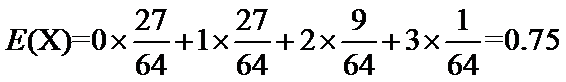
考查方向
解题思路
(1)先表示所求事件再计算其概率(2)写出X的所有可能取值并求出相应概率,列出分布列和计算数学期望。
易错点
所求事件的表示及概率的计算。
如图,在直三棱柱ABC-A1B1C1中,D1E分别为BB1和CC1的中点,AF⊥平面A1DE,其垂足F落在直线A1D上.
21.求证:BC⊥A1D;
22.若A1D=
正确答案
(1)BC⊥A1D;
解析
(1)∵在直三棱柱


又∵


又∵




又∵




而




∴

又∵


考查方向
解题思路
(1)通过证明线面垂直证线线垂直(2)利用空间直角坐标系,求出两个半平面的法向量再计算
易错点
忽视证明线线垂直的条件
正确答案
(2)
解析
(2)由(1)知







∵

则由


则






设平面

由



设平面

由



∴
∴二面角

考查方向
解题思路
(1)通过证明线面垂直证线线垂直(2)利用空间直角坐标系,求出两个半平面的法向量再计算
易错点
忽视证明线线垂直的条件
已知Q为椭圆C:

23.求椭圆C的方程:
24.若直线l:y=kx+m(|k|≤
正确答案
(1)
解析
(1)因为




由题设可知

又点




①②联立解得,

故所求椭圆的方程为
考查方向
解题思路
(1)通过

易错点
线段OM的中点与线段AB的中点重合的转化
正确答案
(2)
解析
(2)设



由


由(1)-(2),得
由线段



又

把(4)(5)(6)代入(3)整理,得
于是由


所以
因为


所以


考查方向
解题思路
(1)通过

易错点
线段OM的中点与线段AB的中点重合的转化
【选修4-1:几何证明选讲】
如图,已知D为以AB为斜边的Rt△ABC的外接圆O上一点,CE⊥AB,BD交AC,CE的交点分别为F,G,且G为BF中点,
27.求证:BC=CD;
28.过点C作圆O的切线交AD延长线于点H,若AB=4,DH =1,求AD的长.
正确答案
(1)BC=CD;
解析
(1)由题意知

又∵



由


∴

∴


考查方向
解题思路
(1)通过弧长相等得出线段相等;(2)通过圆的切割线定理计算AD的长。
易错点
对圆的切割线定理的灵活运用。
正确答案
(2)AD=2
解析
(2)∵

又∵


∴


由(1)知


∴

由切割线定理,得


考查方向
解题思路
(1)通过弧长相等得出线段相等;(2)通过圆的切割线定理计算AD的长。
易错点
对圆的切割线定理的灵活运用。
已知函数f (x)= 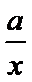
25.若函数f(x)在区间[1,e]上的最小值是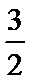
26.当a=1时,设F(x)=f(x)+1+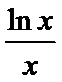
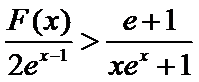
正确答案
(1)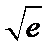
解析
(1)因 为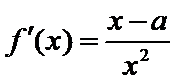
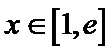
①当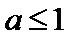
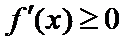
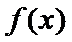
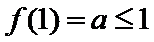
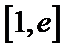
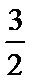
②当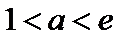
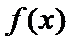
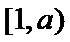
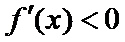
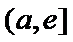
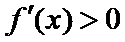
∴函数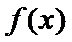
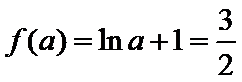
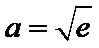
③当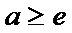
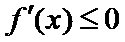
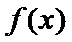
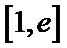
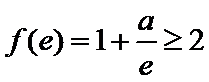
综上所述,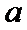
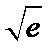
考查方向
解题思路
(1)先对函数进行求导,再对参数进行分类讨论探讨函数的单调性从而研究其最小值及此时a的值 ;(2)通过灵活变形构造新函数的方法证明不等式。
易错点
对参数的分类讨论研究函数的最值。
正确答案
(2)当x>l时,
解析
(2)要证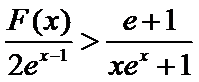
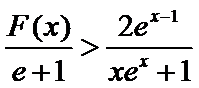
当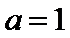
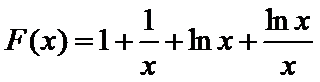
令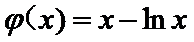
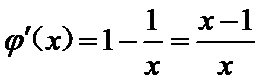
当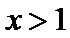
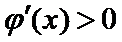
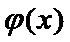
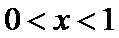
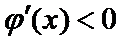
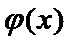
∴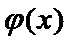
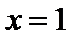
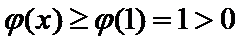
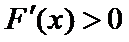
∴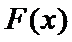
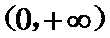
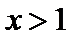
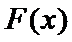
故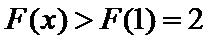
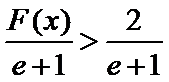
令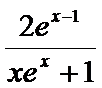
∵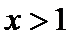
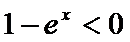
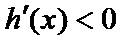
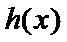
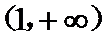
∴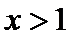
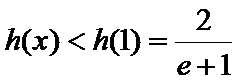
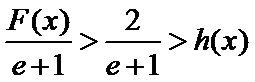
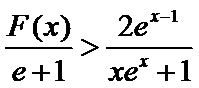
所以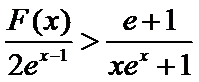
考查方向
解题思路
(1)先对函数进行求导,再对参数进行分类讨论探讨函数的单调性从而研究其最小值及此时a的值 ;(2)通过灵活变形构造新函数的方法证明不等式。
易错点
对参数的分类讨论研究函数的最值。