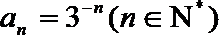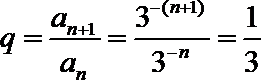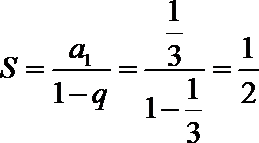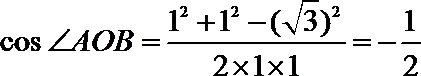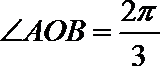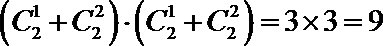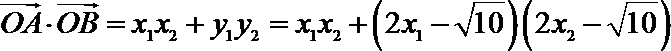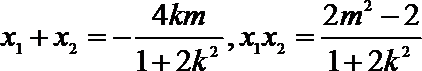- 真题试卷
- 模拟试卷
- 预测试卷
2.方程
正确答案
解析
∵
∴方程

考查方向
本题主要考查了对数方程的解法,考查学生计算能力,属于容易题.
易错点
在对数方程的求解中,将对数式转化成指数式的过程中,特别要注意对数式中的底数、真数、对数与指数式中的底数、幂、指数的对应关系.
知识点
3.设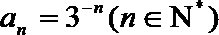
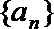
正确答案
解析
∵
∴首项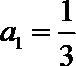
∴数列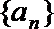
考查方向
本题主要考查无穷等比数列各项和公式,考查学生基础知识的掌握能力,是容易题.
解题思路
先求出数列的首项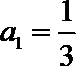
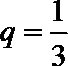
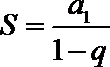
.
易错点
没注意到这是无穷等比数列,其公比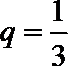
知识点
6.若函数

正确答案
解析
∵
∴方程

∴函数

由图可知
∴
考查方向
本题主要考查函数的性质,考查数形结合、函数与方程的思想,是中档题,在近几年各省市的高考中出现频率很高,常将函数的几个性质结合在一起进行命题.
解题思路
作出函数


易错点
对函数零点概念的不理解,或者不能将函数零点个数转化为两个函数图像四个交点来求解.
知识点
1.设抛物线的顶点在原点,准线方程为
正确答案
解析
∵抛物线的顶点在原点,准线方程为
∴可设抛物线的方程为
∵
∴
∴抛物线的方程为
考查方向
本题考查抛物线标准方程,考查学生基础知识的掌握能力,属于容易题.
易错点
1.对
知识点
4.函数
正确答案
解析
∵
而∴
∴
考查方向
本题主要考查三角化简,是容易题.
解题思路
先逆用二倍角公式,然后用辅助角公式,最后利用三角函数的有界性求得函数的最小值.
易错点
三角公式很多,容易混淆公式的使用;逆用公式易出错.
知识点
5.若函数




正确答案
解析
∵函数


∴以




∴所求解析式为
考查方向
本题考查函数的图像变换,是容易题.
解题思路
函数









易错点
混淆各种函数图像变换.
知识点
7.若


正确答案
16
解析
∵
∴
(当且仅当

∴
考查方向
本题考查基本不等式,是容易题.
解题思路

易错点
当一个整数式子与一个分式式子在一个题中出现时,求一个式子的最值,常将两个式子相乘,展开,然后利用基本不等式求解.利用基本不等式求最值要注意:一正、二定、三相等.
知识点
8.若三条直线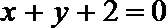
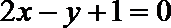
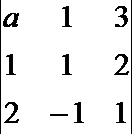
正确答案
0
解析
解方程组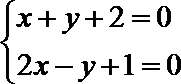
∴行列式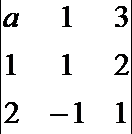
考查方向
本题主要考查两直线交点的求法、三条直线相交于一点的解题策略,考查三阶行列式的运算法则,考查计算能力,是容易题.
解题思路
先求x+y+2=0和2x-y+1=0的交点,代入直线ax+y+3=0,即可得到a的值.再利用行列式的计算法则,展开表达式,化简即可.
易错点
混淆行列式与矩阵.
知识点
9.
正确答案
28
解析
令

∴
考查方向
本题主要考查多项式的系数和,考查分析问题的能力,属于容易题.
解题思路
要求多项式的系数和,实际上就是当
易错点
将整式展开后求各项系数的和,会增加计算量,并且容易出错.
知识点
10.已知四面体

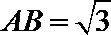


正确答案
解析
由四面体

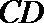

球的半径
∴
∴
∴
∴



考查方向
本题考查球面距离及其相关计算,考查空间想象能力、计算、逻辑思维能力,是中档题.
解题思路
先求球半径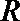

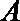


易错点

知识点
12.正四面体的四个面上分别写有数字0,1,2,3把两个这样的四面体抛在桌面上,则露在外面的6个数字之和恰好是9的概率为___________.
正确答案
解析
由题意,试验发生所包含的事件是2个均匀的正四面体与桌面接触,共有4×4=16种情况.一个正四面体的四个面的数字和为6,则露在外面的6个数字之和恰好是9即与桌面接触两个面的数字和为3,它包括0+3、1+2、2+1、3+0四种情况.∴所求概率为
考查方向
本题考查等可能事件的概率计算,是容易题,在近几年各地高考中频频出现.
解题思路
先求试验所包含的事件的所有种数,然后寻找符合要求的试验种数,即可得到概率.
易错点
解题的关键是正确运用列举法,分析得到基本事件的个数.
知识点
13.设




正确答案
解析
由题意,设


∵

∴
∴
又∵

若
∴


∴
∴
若

考查方向
本题考查复数代数形式的混合运算、实数的条件、以及利用周期性求和,考查化简计算能力,是中档题.
解题思路
根据实系数二次方程的虚根成对出现,设









易错点
对条件“

知识点
11.已知函数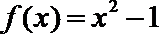
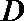
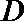
正确答案
9
解析
∵函数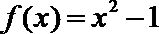
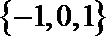
由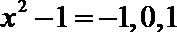
∴函数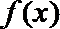
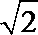
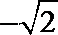
∴函数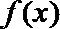
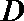
共9种可能,故这样的集合
考查方向
本题主要考查函数的概念及其构成元素、排列组合的知识,考查学生分析问题的能力,是容易题.
解题思路
由题意知,函数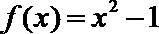
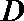
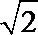
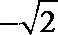
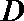
易错点
再求得定义域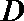
知识点
14. 已知




正确答案
解析
如图所示,设


由三角形外接圆的性质可得
∴
∵

两边与

∴
由正弦定理可得
化简得
又∵
∴
又∵
∴
∴
考查方向
本题综合考查了三角形外接圆的性质、垂径定理、正弦定理、数量积运算性质、两角和差的余弦公式、三角函数基本关系式等基础知识与基本技能方法,考查了分析问题和解决问题的能力,属于难题.这类问题在近几年各省市的高考试卷中出现频率很高,以平面向量为载体,可以与三角、函数、数列、解析几何等知识结合交汇命题.
解题思路
取




由向量的三角形法则可得






易错点
对条件
知识点
15.已知向量


正确答案
解析
设向量




选项A:
选项B:

选项C:

选项D:由A选项的证明可知







考查方向
本题考查平面向量垂直与平行的条件、向量数量积的运算,是容易题.
解题思路
向量垂直用两个向量的数量积为零来判定,向量平行用向量平行的条件判定.
易错点
混淆平面向量垂直与平行的条件,对充分性和必要性认识不足.
知识点
16.设


正确答案
解析
(1)若
当

即“


(2)若
当

即“


综上所述,“

考查方向
本题考查充分条件、必要条件、充分必要条件的判断以及不等式的性质,是容易题,涉及充分必要条件的问题在近几年的各省高考题中出现的频率非常高,它可以与高中数学每一个章节每一个知识点相结合进行命题,是高考的热点问题.
解题思路
根据不等式的性质,先判断“





易错点
对充分性和必要性的认识不足,混淆不等式的各种性质以及各性质需要的前提条件.
知识点
17.设






正确答案
解析
由题意可得
由线性规划的知识可得:可行域为直线

考查方向
本题考查了复数代数表示及其几何意义和线性规划的可行域,属于中档题.在近几年的各省高考题中出现的频率较低.
解题思路
由题意可得
易错点
线性规划可行域容易选错.
知识点
18.设函数









正确答案
解析
在
若
则

∴

∴
∴
故选C.
考查方向
本题考查函数的性质,考查即时学习能力,是中档题.新定义的学习型问题,在近几年各省市高考中出现的频率很高,常以压轴题的形式出现,整合函数、数列、解析几何、三角、向量等知识,体现数学多种思想方法.
解题思路
先求


易错点
对新定义对称中心的不理解.
知识点
20.已知实数


(1)求实数
(2)求

正确答案
(1)
(2)当




解析
(1)设


即

(2)因为

当


当




考查方向
本题考查指数不等式、函数性质、函数最值的求解以及对数运算法则,考查计算能力,是容易题.
解题思路
题(1),换元法解不等式,先求出所换元的取值范围,再利用指数函数的性质解简单指数不等式;
题(2),将函数


易错点
换元法求解过程容易忽略所换元的取值范围.
知识点
19.在三棱锥




求证

正确答案
证明略;

解析
∵

∴


又∵
∴
故

在

∴
又在

∴
又∵

∴

考查方向
本题主要考查立体几何中两直线相互垂直的判定以及简单多面体的体积公式,考查逻辑推理能力以及计算能力,是容易题.
解题思路

易错点
线线垂直与线面垂直的相互转化,条件缺一不可.题中的证明,在证明线面垂直时,必须是平面外的直线分别垂直于平面上的两条相交直线,才能得到线面垂直.
知识点
21.节能环保日益受到人们的重视,水污染治理也已成为“十三五”规划的重要议题.某地有三家工厂,分别位于矩形














(1)将

(2)试确定
正确答案
(1)

(2)点





解析
(1)由已知得
即

(2)记


解得

由于







考查方向
本题以实际问题为背景,主要考查函数解析式的构建以及函数最值的求解,考查数学建模的能力,是中档题.以实际问题为背景的生活中的优化问题,这类问题在近几年各省市的高考试卷中频频出现,是高考的热点问题.这类问题往往涉及到建立函数关系式和函数的最值,一般先设自变量、因变量,建立函数关系式,并确定其定义域,求最值时可利用三角函数的有界性、函数的单调性,也可直接利用导数求最值,要掌握求最值的方法和技巧.也注意结果应与实际情况相符合.
解题思路
先建立函数,再利用三角函数的有界性求
易错点
建立函数过程中,容易遗忘定义域,还要注意实际情况;求最值的有多种方法,还要注意结果应与实际情况相符合.
知识点
22.给定数列









(1)对于数列:3,4,7,1,求出相应的
(2)若







①设

②若数列




正确答案
(1)
(2)①证明略;②
解析
(1)当

同理可得
(2)①当


当
两式相减得

所以,数列


②由①知:
又
由于
所以由
所以

因为

由

但




考查方向
本题考查数列的综合应用,突出考查考查推理论证与抽象思维的能力,是难题.数列的综合应用在近几年各省市的高考试卷中频频出现,是高考的热点问题,往往以等差数列、等比数列为载体,涉及递推公式、通项公式、前项和,结合数列单调性、数列恒成立等知识交汇命题.
解题思路
题(1),当


题(2)①,利用等比数列的定义证明











题(2)②,由①得到





易错点
对含有






知识点
23.已知直线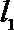
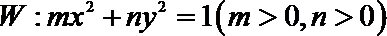

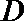

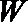
(1)若直线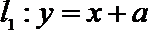

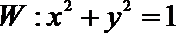
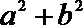
(2)若直线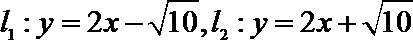
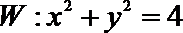
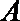
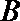
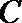
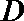

(3)求证:椭圆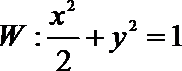
正确答案
(1)2;
(2)证明略;
(3)证明略,面积为
解析
(1)由于直线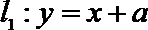
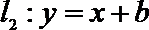

所以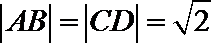
在等腰直角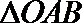
圆心

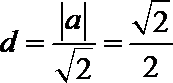
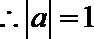
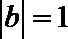

(2)由题知,直线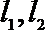
因为圆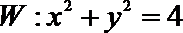

所以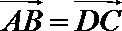
故四边形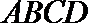
易知,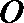
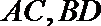
联立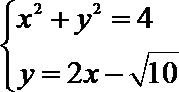
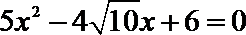
由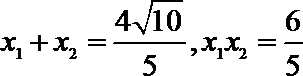
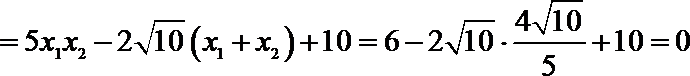
所以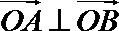
于是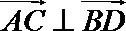
因为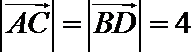
所以四边形
(3)证明:假设椭圆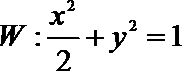
当直线
设直线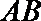
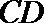
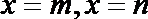
因为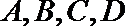
所以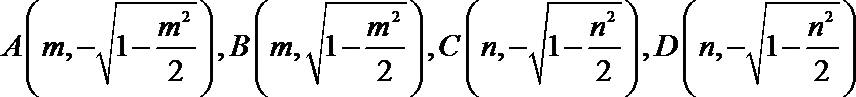
由四边形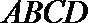
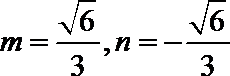
直线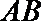
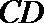
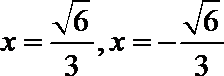
正方形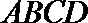

当直线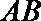
设直线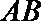
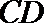
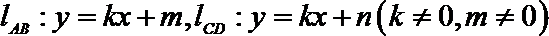
显然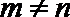
设
联立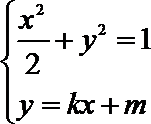
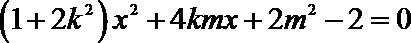
所以
代人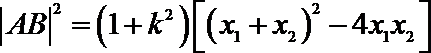
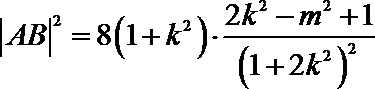
同理可得
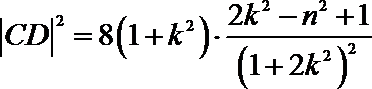
因为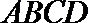
所以
解得
因为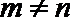
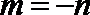
因此,直线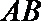
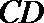
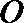
所以原点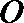
(由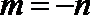
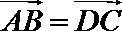

由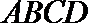
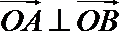
即
代人得
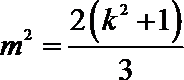
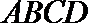
由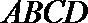

因为直线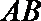
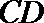
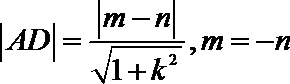
故
但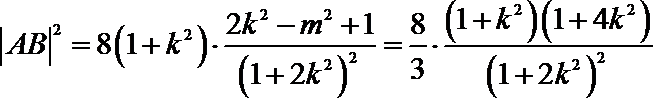
由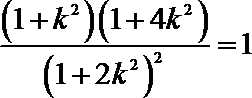
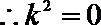

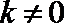
所以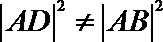
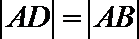
即当直线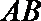
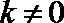
综上所述,椭圆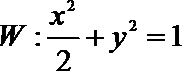
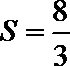
考查方向
本题主要考查直线与圆锥曲线的综合应用,考查学生分析问题解决问题的能力、逻辑推理能力,是难题.解析几何的综合应用在近几年各省市的高考试卷中频频出现,是高考的热点问题,往往以直线、圆、椭圆、双曲线、抛物线为载体,涉及各类曲线的定义与方程、各类曲线的性质,与曲线的轨迹方程的求解、直线与圆锥曲线的位置关系等知识交汇命题.
解题思路
题(1),先找到两直线分单位圆成长度相等的四段弧的位置,求得所截得的弦长,然后利用原点到直线距离公式求得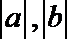
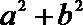
题(2),先证四边形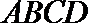
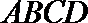
题(3),分类讨论说明椭圆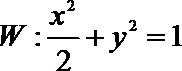
易错点
找不到直线与圆或者椭圆的正确的位置关系,从而无法解题.