- 真题试卷
- 模拟试卷
- 预测试卷
6.在
正确答案
解析
Tr+1=



知识点
9.从个位数与十位数之和为奇数的两位数中任取一个,其个位数为0的概率是( )
正确答案
解析
在个位数与十位数之和为奇数的两位数中:
(1)当个位数是偶数时,由分步计数乘法原理知,共有5×5=25个;
(2)当个位数是奇数时,由分步计数乘法原理知,共有4×5=20个.
综上可知,基本事件总数共有25+20=45(个),
知识点
10.样本(x1,x2,…,xn)的平均数为






正确答案
解析
由已知,得x1+x2+…+xn=n






整理,得(

∵
∴αm+(α-1)n=0,即

又0<α<


又n,m∈N+,∴n<m.
知识点
1.设集合A={x|1<x<4},集合B={x|x2-2x-3≤0},则A∩(∁RB)=( ).
正确答案
解析
解:由已知得,B={x|x2-2x-3≤0}={x|-1≤x≤3},
所以∁RB={x|x<-1,或x>3}.
所以A∩(∁RB)={x|3<x<4}.
知识点
2.i是虚数单位,复数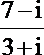
正确答案
解析
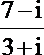
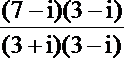
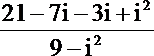
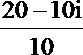
知识点
3.设φ∈R,则“φ=0”是“f(x)=cos(x+φ)(x∈R)为偶函数”的( )
正确答案
解析
φ=0时,f(x)=cos x,f(-x)=f(x),∴f(x)为偶函数;若f(x)为偶函数,则f(0)=±1,∴cos φ=±1,∴φ=kπ(k∈Z).∴是充分而不必要条件.
知识点
5.函数f(x)=2x+x3-2在区间(0,1)内的零点个数是( )
正确答案
解析
f'(x)=2xln 2+3x2,在(0,1)上f'(x)>0恒成立,
∴f(x)在区间(0,1)上单调递增.
又∵f(0)=20+03-2=-1<0,f(1)=21+13-2=1>0,
∴f(x)在区间(0,1)上存在一个零点.
知识点
4.阅读下边的程序框图,运行相应的程序,当输入x的值为-25时,输出x的值为( )
正确答案
解析
x=|-25|>1,x=
x=|4|>1,x=
x=|1|>1不成立,
∴x=2×1+1=3.
知识点
8.某几何体的三视图如图所示,它的体积为( ).
正确答案
解析
由三视图知该几何体是由圆锥和圆柱构成的组合体,示意图如图所示,
∴该几何体的体积为V=V圆锥+V圆柱=

知识点
7.已知变量x,y满足约束条件
正确答案
解析
解:由约束条件作出可行域,如图,
∴可得最优解
∴zmax=3×3+2=11.
知识点
13.椭圆

正确答案
解析
因为A,B为左、右顶点,F1,F2为左、右焦点,
所以|AF1|=a-c,|F1F2|=2c,|BF1|=a+c.
又因为|AF1|,|F1F2|,|BF1|成等比数列,
所以(a-c)(a+c)=4c2,即a2=5c2,
所以离心率e=

知识点
11.计算定积分
正确答案
解析




知识点
14.曲线y=x3-x+3在点(1,3)处的切线方程为______.
正确答案
2x-y+1=0
解析
由y=x3-x+3得y'=3x2-1,∴切线的斜率k=y'|x=1=3×12-1=2,∴切线方程为y-3=2(x-1),即2x-y+1=0.
知识点
12.设数列{an},{bn}都是等差数列,若a1+b1=7,a3+b3=21,则a5+b5=______.
正确答案
35
解析
∵{an},{bn}均是等差数列,根据等差数列的性质a1+a5=2a3,b1+b5=2b3,即a5=2a3-a1,b5=2b3-b1,∴a5+b5=2(a3+b3)-(a1+b1)=2×21-7=35.
知识点
15.请从以下两题中任选一题作答。
(1)(坐标系与参数方程选做题)曲线C的直角坐标方程为x2+y2-2x=0,以原点为极点,x轴的正半轴为极轴建立极坐标系,则曲线C的极坐标方程为_____.
(2)(不等式选做题)在实数范围内,不等式|2x-1|+|2x+1|≤6的解集为______.
正确答案
(1)ρ=2cos θ
(2)
解析
解析已在路上飞奔,马上就到!
知识点
17.某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进16枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式;
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
以100天记录的各需求量的频率作为各需求量发生的概率.
①若花店一天购进16枝玫瑰花,X表示当天的利润(单位:元),求X的分布列、数学期望及方差;
②若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由.
正确答案
解:(1)当日需求量n≥16时,利润y=80.
当日需求量n<16时,利润y=10n-80.
所以y关于n的函数解析式为
y=
(2)①X可能的取值为60,70,80,并且P(X=60)=0.1,P(X=70)=0.2,P(X=80)=0.7.
X的分布列为
X的数学期望为
EX=60×0.1+70×0.2+80×0.7=76.
X的方差为DX=(60-76)2×0.1+(70-76)2×0.2+(80-76)2×0.7=44.
②答案一:
花店一天应购进16枝玫瑰花.理由如下:
若花店一天购进17枝玫瑰花,Y表示当天的利润(单位:元),那么Y的分布列为
Y的数学期望为EY=55×0.1+65×0.2+75×0.16+85×0.54=76.4.
Y的方差为DY=(55-76.4)2×0.1+(65-76.4)2×0.2+(75-76.4)2×0.16+(85-76.4)2×0.54=112.04.
由以上的计算结果可以看出,DX<DY,即购进16枝玫瑰花时利润波动相对较小.
另外,虽然EX<EY,但两者相差不大.
故花店一天应购进16枝玫瑰花.
答案二:
花店一天应购进17枝玫瑰花.理由如下:
若花店一天购进17枝玫瑰花,Y表示当天的利润(单位:元),那么Y的分布列为
Y的数学期望为EY=55×0.1+65×0.2+75×0.16+85×0.54=76.4.
由以上的计算结果可以看出,EX<EY,即购进17枝玫瑰花时的平均利润大于购进16枝时的平均利润.故花店一天应购进17枝玫瑰花.
解析
解析已在路上飞奔,马上就到!
知识点
18.已知数列{an}的前n项和Sn=kcn-k(其中c,k为常数),且a2=4,a6=8a3.
(1)求an;
(2)求数列{nan}的前n项和Tn.
正确答案
解:(1)由Sn=kcn-k,得an=Sn-Sn-1=kcn-kcn-1(n≥2),
由a2=4,a6=8a3,得kc(c-1)=4,kc5(c-1)=8kc2(c-1),
解得
于是an=2n.
(2)Tn=

Tn=2+2·22+3·23+4·24+…+n·2n,
Tn=2Tn-Tn=-2-22-23-24-…-2n+n·2n+1=-2n+1+2+n·2n+1=(n-1)2n+1+2.
解析
解析已在路上飞奔,马上就到!
知识点
19.在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,FC⊥平面ABCD,AE⊥BD,CB=CD=CF.
(1)求证:BD⊥平面AED;
(2)求二面角F-BD-C的余弦值.
正确答案
(1)证明:因为四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,
所以∠ADC=∠BCD=120°.
又CB=CD,所以∠CDB=30°.
因此∠ADB=90°,AD⊥BD.
又AE⊥BD,且AE∩AD=A,AE,AD⊂平面AED,
所以BD⊥平面AED.
(2)解法一:由(1)知AD⊥BD,所以AC⊥BC.
又FC⊥平面ABCD,
因此CA,CB,CF两两垂直,
以C为坐标原点,分别以CA,CB,CF所在的直线为x轴,y轴,z轴,
建立如图所示的空间直角坐标系,不妨设CB=1,
则C(0,0,0),B(0,1,0),D
因此


设平面BDF的一个法向量为m=(x,y,z),
则m·

所以x=

取z=1,则m=(
由于
则cos<m,



所以二面角F-BD-C的余弦值为
解法二:
取BD的中点G,连接CG,FG,
由于CB=CD,因此CG⊥BD.
又FC⊥平面ABCD,BD⊂平面ABCD,
所以FC⊥BD.
由于FC∩CG=C,FC,CG⊂平面FCG,
所以BD⊥平面FCG.故BD⊥FG.
所以∠FGC为二面角F-BD-C的平面角.
在等腰三角形BCD中,由于∠BCD=120°,
因此CG=
又CB=CF,
所以GF=

故cos∠FGC=
因此二面角F-BD-C的余弦值为
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆


(1)求椭圆的离心率;
(2)设A为椭圆的左顶点,O为坐标原点.若点Q在椭圆上且满足|AQ|=|AO|,求直线OQ的斜率的值.
正确答案
(1)解:因为点P




于是e2=



(2)解:设直线OQ的斜率为k,则其方程为y=kx,设点Q的坐标为(x0,y0).
由条件得


由|AQ|=|AO|,A(-a,0)及y0=kx0,得(x0+a)2+k2

故x0=

由(1)知


所以直线OQ的斜率k=±
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数f(x)满足f(x)=f'(1)ex-1-f(0)x+
(1)求f(x)的解析式及单调区间;
(2)若f(x)≥
正确答案
解:(1)由已知得f'(x)=f'(1)ex-1-f(0)+x.
所以f'(1)=f'(1)-f(0)+1,即f(0)=1.
又f(0)=f'(1)e-1,所以f'(1)=e.
从而f(x)=ex-x+
由于f'(x)=ex-1+x,
故当x∈(-∞,0)时,f'(x)<0;
当x∈(0,+∞)时,f'(x)>0.
从而,f(x)在(-∞,0)单调递减,在(0,+∞)单调递增.
(2)由已知条件得ex-(a+1)x≥b.①
(ⅰ)若a+1<0,则对任意常数b,当x<0,且x<
(ⅱ)若a+1=0,则(a+1)b=0.
(ⅲ)若a+1>0,设g(x)=ex-(a+1)x,
则g'(x)=ex-(a+1).
当x∈(-∞,ln(a+1))时,g'(x)<0;
当x∈(ln(a+1),+∞)时,g'(x)>0.
从而g(x)在(-∞,ln(a+1))单调递减,在(ln(a+1),+∞)单调递增.
故g(x)有最小值g(ln(a+1))=a+1-(a+1)ln(a+1).
所以f(x)≥
b≤a+1-(a+1)ln(a+1).②
因此(a+1)b≤(a+1)2-(a+1)2ln(a+1).
设h(a)=(a+1)2-(a+1)2ln(a+1),
则h'(a)=(a+1)(1-2ln(a+1)).
所以h(a)在(-1,
在(
故h(a)在a=
从而h(a)≤

当a=

故f(x)≥
综合得,(a+1)b的最大值为
解析
解析已在路上飞奔,马上就到!
知识点
16.已知a,b,c分别为△ABC三个内角A,B,C的对边,acos C+
(1)求A;
(2)若a=2,△ABC的面积为
正确答案
解:(1)由acos C+
sin Acos C+
因为B=π-A-C,
所以
由于sin C≠0,所以sin

又0<A<π,故A=
(2)△ABC的面积S=

而a2=b2+c2-2bccos A,故b2+c2=8.
解得b=c=2.
解析
解析已在路上飞奔,马上就到!


















