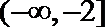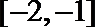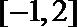- 真题试卷
- 模拟试卷
- 预测试卷
6.已知等差数列





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若圆C: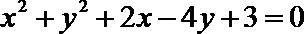

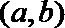
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 对于函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知函数①

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 关于


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
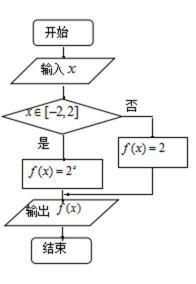
3.阅读下面程序框图,如果输出的函数值在区间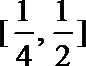
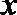
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.平面四边形







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.直线











正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设F1, F2分别为双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数f(x)是定义在R上的以4为周期的函数,”当x∈(-1,3]时,f(x)=


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知 


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.一个几何体的三视图如图所示,则这个几何体的表面积与其外接球面积之比为________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.在等差数列





正确答案
-2013
解析
解析已在路上飞奔,马上就到!
知识点
16.设函数f(x)=x2-1,对任意x∈[

正确答案
(-∞,-

解析
解析已在路上飞奔,马上就到!
知识点
14.设

正确答案
160
解析
解析已在路上飞奔,马上就到!
知识点
18.设公比大于零的等比数列










(Ⅰ)求数列

(Ⅱ)设


正确答案
解:(Ⅰ)由


又

则得
所以

(Ⅱ)


设,若数列

则

即

当



解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆E:


(I)求椭圆E的标准方程;
(Ⅱ)设Q(2,0),过点(-1,0)的直线l交椭圆E于M、N两点.
(i)当
(ii)记ΔQMN的面积为S,若对满足条件的任意直线l,不等式S
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,四棱柱


(Ⅰ)从下列①②③三个条件中选择一个做为
①
②
③
(Ⅱ)设四棱柱




正确答案
解:(Ⅰ)条件②

证明如下:




∵


若条件②成立,即
∵


又


(Ⅱ)由已知,得

设




∴



以


如图所示.
设


则






设


令



又


令





因为函数


所以
又




解析
解析已在路上飞奔,马上就到!
知识点
21.分已知函数



(Ⅰ)当

(Ⅱ)当

(Ⅲ)当



正确答案
解:(Ⅰ)依题意,


当








所以


所以


(Ⅱ)
当




令

当

当




令

综上所述: 当




当


当



(Ⅲ)由(Ⅱ)可知,当





因为存在

所以

又



所以

解析
解析已在路上飞奔,马上就到!
知识点
请考生在第(22)、(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题记分
22.如图,⊙O1与⊙O2相交于A、B两点,过点A作⊙O1的切线交⊙O2于点C,过点B作两圆的割线,分别交⊙O1、⊙O2于点D、E,DE与AC相交于点P.
(1)求证:AD//EC;
(2)若AD是⊙O2的切线,且PA=6,PC =2,BD =9,求AD的长。
23.在平面直角坐标系







(Ⅰ)求曲线
(Ⅱ)设直线





24.已知不等式

(Ⅰ )求
(Ⅱ )若

正确答案
22.(1)证明:连接




(2)





又







23.解:(Ⅰ)由

当

对应直角坐标方程为:




∴曲线

(Ⅱ)把直线


即



∵直线



24.解:(Ⅰ)依题意,当


经检验,
(Ⅱ)由(Ⅰ)知
根据柯西不等式得
所以
当且仅当



因此

解析
解析已在路上飞奔,马上就到!
知识点
17.已知










(Ⅰ)若



(Ⅱ)若



正确答案
解(Ⅰ)









解得



(Ⅱ)在







又






解析
解析已在路上飞奔,马上就到!