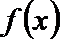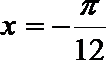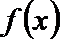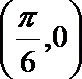理科数学成都市2013年高三试卷

精品

单选题
填空题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共10小题，每小题5分，共50分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

3．“数列为常数列”是“数列既是等差数列又是等比数列”的（）

A充分不必要条件

B必要不充分条件

C充要条件

D既不充分也不必要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

充要条件的判定等差数列的判断与证明等比数列的判断与证明

题型：单选题

分值: 5分

4．命题P：若x,y∈R．则｜x｜+ ｜y｜＞1是｜x+y｜ >1的充分而不必要条件；命题q ：函数y=的定义域是（一∞，一1］U［3，＋∞），则（）

A“pVq”为假

B“pq”为真

C“”为真

D“”为真

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

含有逻辑联结词命题的真假判断函数的定义域及其求法

题型：单选题

分值: 5分

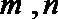
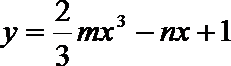
7．将一颗骰子抛掷两次，所得向上点数分别为，则函数在上为增函数的概率是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质古典概型的概率

题型：单选题

分值: 5分

8．已知函数f(x)的定义域为［－1,4］，部分对应值如下表，f(x)的导函数的图象如下图所示。当1＜a<2时，函数y=f(x)－a的零点的个数为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数零点的判断和求解

题型：单选题

分值: 5分

2．已知向量，，且//，则等于（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程

题型：单选题

分值: 5分

9．已知等差数列中，，记数列的前项和为，若，对任意的成立，则整数的最小值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

题型：单选题

分值: 5分

5．已知函数，则（）

A函数的周期为

B函数在区间上单调递增

C函数的图象关于直线对称

D函数的图象关于点对称

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法正弦函数的单调性正弦函数的对称性三角函数中的恒等变换应用

题型：单选题

分值: 5分

6．已知直线，平面，且，，给出下列四个命题：

①若∥，则；

②若，则∥；

③若，则∥；

④若∥，则．

其中真命题的个数为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

命题的真假判断与应用空间中直线与直线之间的位置关系空间中直线与平面之间的位置关系平面与平面之间的位置关系

题型：单选题

分值: 5分

1．设集合，，则（）

B（3,4）

C（-2,1）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

10．设是正三棱锥的底面⊿的中心，过的动平面与交于，与、的延长线分别交于、，则（）

A有最大值而无最小值

B有最小值而无最大值

C无最大值也无最小值

D是与平面无关的常数

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的值域棱柱、棱锥、棱台的体积

填空题本大题共5小题，每小题5分，共25分。把答案填写在题中横线上。

题型：填空题

分值: 5分

12．若展开式的常数项为60，则常数的值为．

正确答案

（-1,2）

解析

解析已在路上飞奔，马上就到！

知识点

求二项展开式的指定项或指定项的系数

题型：填空题

分值: 5分

14．若不等式上恒成立，则实数a的取值范围为。

正确答案

a≥1

解析

解析已在路上飞奔，马上就到！

知识点

不等式恒成立问题

题型：填空题

分值: 5分

15．由9个正数组成的数阵每行中的三个数成等差数列，且，，成等比数列．给出下列结论：

①第二列中的必成等比数列；

②第一列中的不一定成等比数列；

③；

④若9个数之和大于81，则 >9．

其中正确的序号有．（填写所有正确结论的序号）．

正确答案

①②③

解析

解析已在路上飞奔，马上就到！

知识点

等比数列的判断与证明等比数列的性质及应用等差数列与等比数列的综合

题型：填空题

分值: 5分

13．已知实数x,y满足，则z=2|x|+y的取值范围。

正确答案

[-1,1]

解析

解析已在路上飞奔，马上就到！

知识点

其它不等式的解法

题型：填空题

分值: 5分

11．输入x=2，运行下图的程序输出的结果为。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线与平面平行的判定与性质

简答题（综合题）本大题共75分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

17．某高中为了推进新课程改革，满足不同层次学生的需求，决定从高一年级开始，在每周的周一、周三、周五的课外活动期间同时开设数学、物理、化学、生物和信息技术辅导讲座，每位有兴趣的同学可以在期间的任何一天参加任何一门科目的辅导讲座，也可以放弃任何一门科目的辅导讲座。（规定：各科达到预先设定的人数时称为满座，否则称为不满座）统计数据表明，各学科讲座各天的满座的概率如下表：

根据上表：

（1）求数学辅导讲座在周一、周三、周五都不满座的概率；

（2）设周三各辅导讲座满座的科目数为，求随机变量的分布列和数学期望。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

古典概型的概率离散型随机变量及其分布列、均值与方差

题型：简答题

分值: 13分

20．已知数列满足，（）。

（Ⅰ）求数列的通项公式；

（Ⅱ）设，求的前n项和；

（Ⅲ）设，数列的前n项和，求证：对。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由递推关系式求数列的通项公式裂项相消法求和数列与不等式的综合

题型：简答题

分值: 12分

19．函数，．

（Ⅰ）当时，求函数在上的最大值；

（Ⅱ）如果函数在区间上存在零点，求的取值范围．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

对数函数的定义

题型：简答题

分值: 12分

18．如图所示，四棱锥P－ABCD的底面是边长为1的正方形，PA⊥CD，PA = 1，PD＝，E为PD上一点，PE = 2ED．

（Ⅰ）求证：PA 平面ABCD；

（Ⅱ）求二面角D－AC－E的余弦值；

（Ⅲ）在侧棱PC上是否存在一点F，使得BF // 平面AEC？若存在，指出F点的位置，并证明；若不存在，说明理由．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线与平面平行的判定与性质直线与平面垂直的判定与性质线面角和二面角的求法

题型：简答题

分值: 12分

16．已知向量，设函数＋

（1）若，f(x)=,求的值；

（2）在△ABC中，角A，B，C的对边分别是，且满足，求f(B)的取值范围．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平行关系的综合应用

题型：简答题

分值: 14分

21．已知函数．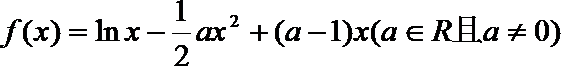

（I）求函数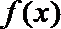的单调递增区间；

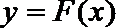
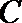
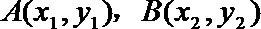
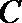
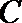
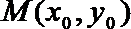
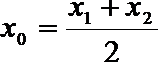
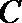
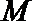
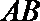
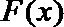
（II）记函数的图像为曲线．设点是曲线上不同两点．如果在曲线上存在点使得：①；②曲线在点处的切线平行于直线,则称函数存在“中值相依切线”．

试问：函数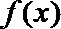是否存在“中值相依切线”，请说明理由．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷