- 真题试卷
- 模拟试卷
- 预测试卷
8.某几何体的三视图如图所示,该几何体的体积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.执行如图所示的程序框图,输出的S值为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知命题



①
②
③
④
其中正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.向量




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.在复平面内,复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.在







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.点







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.设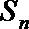
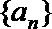
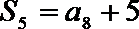
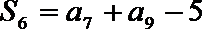
正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
10.已知双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.设直线





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.如图,⊙ 









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.过抛物线



正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
14.抛物线





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在直角坐标系









正确答案

解析
解析已在路上飞奔,马上就到!
知识点
17.在








(1)求
(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知抛物线

(1)当


(2)若



正确答案
(1)抛物线
由已知
联立

所以
(2)联立

因为A与O不重合,故
所以
即
即直线过定点(4,0)
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数

(1)求

(2)若

(3)若





正确答案
(1)
由


(2)函数
由(1)可得
令
因为


所以当

所以单调递增区间为


当
所以单调递增区间为

(3)当
所以
因为函数


所以
要是存在
只需要
又因为

解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆



(1)求椭圆
(2)已知








正确答案
(1)因为

又
所以
所以 椭圆

(2)当直线




所以
当直线

则直线

由
即
所以
即
所以
所以

综上,

解析
解析已在路上飞奔,马上就到!





























































