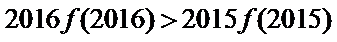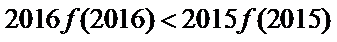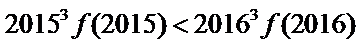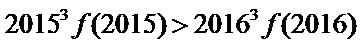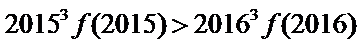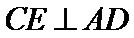- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合

正确答案
解析
M={x/-1<x<2},N=R,所以选B
考查方向
集合的运算,解不等式
解题思路
先求出集合M然后算集合M和集合N的交集
易错点
对集合的概念和性质掌握不牢固
教师点评
集合的运算常和不等式一起结合考查
知识点
2.若复数


正确答案
解析
由题意可知原式=
所以a=-1
考查方向
复数的运算,虚数单位的意义
解题思路
按照复数的性质和运算规则计算
易错点
不理解虚数单位i的特点
教师点评
一定要记住
知识点
3.式子
正确答案
解析
=
所以当且仅当而相等时,等号成立,所以此题选C
考查方向
三角函数的恒等变形
解题思路
直接通分后化成一个分式的情况,然后讨论其最值。
易错点
化简过程错误
知识点
4.如图,在正方形

正确答案
解析
由题意可知,正方形的面积为1
阴影部分的面积
所以由集合概型可以知道,选B
考查方向
几何概型求概率
易错点
不会计算阴影部分的面积
教师点评
利用几何概型求概率关键在于求不规则图形的面积
知识点
7.已知等差数列





正确答案
解析
根据题意可知,
由
所以
考查方向
等差数列的前N项和,等差数列的最大项
解题思路
根据题意,前五项和和前九项和相等,所以可以得到前7项和最大
易错点
等差数列性质掌握不好
知识点
8.某大学的




正确答案
解析
分类讨论,有2种情形:
孪生姐妹乘坐甲车:则有
孪生姐妹不乘坐甲车:则有
所以共有24种,所以选A
考查方向
排列和组合的应用
解题思路
分类讨论,求出孪生姐妹乘坐甲车的情况,再求出孪生姐妹不乘坐甲车的情况
易错点
考虑情况不全面
知识点
5.已知中心在原点的双曲线



正确答案
解析
依题意可知,
从而
所以选B
考查方向
双曲线的离心率 双曲线的准线方程
解题思路
根据等量关系,求解出参数的值,进而得到双曲线的离心率和准线方程
易错点
计算错误,相关公式记忆混淆
知识点
6.执行如图所示的程序框图,若输入
正确答案
解析
第一次循环后,s=1,i=2
第二次循环后,s=2,i=3
第三次循环后,s=4,i=4
第四次循环后,s=7,i=5
第五次循环后,s=11,i=6,
故输出11,所以选C
考查方向
程序框图
解题思路
根据程序框图按照步骤执行程序
易错点
判断循环结束条件错误
知识点
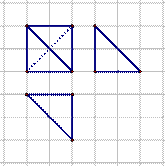
11.如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则几何体的体积为( )
正确答案
解析
由题意可知,原几何体为三棱锥,如图所示
所以
所以选D
考查方向
空间几何体的还原与计算
解题思路
根据三视图还原成立体图,然后求体积
易错点
还原立体图时错误
知识点
12.已知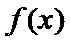
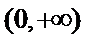
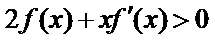
正确答案
解析
构造函数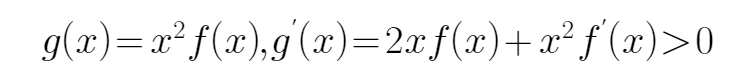
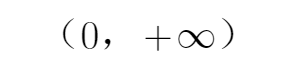
集合不等式的性质,选D
考查方向
利用导数判断函数的单调性和单调区间
解题思路
先构造函数,然后求导,然后判断单调性进而证明不等式
易错点
构造不出来正确的函数
教师点评
解决此类问题关键在于构造正确的函数,而构造函数在于对一些式子有“敏感度”学生要多做相关题型的题,总结经验
知识点
9.
正确答案
解析
所以当且仅当r=5时,-252为常数项,故选A
考查方向
二项式的展开式
解题思路
根据二项式的展开式,找到常数项,然后求得
易错点
二项式展开公式记忆混淆,计算错误
知识点
10.命题

正确答案
解析
由题意可知,命题p为真,命题q为假,所以可知p或q,非p或非q为真,p且非q都是真命题,只有p且q为假命题。
考查方向
含有逻辑联结词命题的真假判断
解题思路
先判断命题p和q的真假,然后结合选项判断
易错点
判断命题真假时错误
知识点
某校课改实行选修走班制,现有甲,乙,丙,丁四位学生准备选修物理,化学,生物三个科目.每位学生只选修一个科目,且选修其中任何一个科目是等可能的.
21.恰有2人选修物理的概率;
22.选修科目个数
正确答案
详见解析
解析
所有可能的选修方式有34种,恰有2人选修物理的方式
考查方向
随机事件发生的概率
解题思路
先求出所有可能的情况,然后求出恰有2人选修物理的情况,二者的比例为发生的概率
易错点
考虑问题不全面,有重或有漏
正确答案
详见解析
解析
ξ的所有可能值为1,2,3.又
综上知,ξ有分布列
ξ 1 2 3
从而有
考查方向
随机变量的分布列,随机变量的数学期望
解题思路
先求出随机变量的所有情况,然后分别算出对应的概率,进而求出分布列和数学期望
易错点
计算错误。分布列考虑情况不全面
教师点评
求随机变量分布列时,要注意书写步骤,计算也要准确
已知函数








17.分别求
18.记


正确答案
解析
由题意可知,
考查方向
求数列的通项公式
解题思路
根据所给定义求函数的通项公式
易错点
对新定义的概念理解不透彻
正确答案
详见解析
解析
依题意,

当


所以
则


令

两式相减得
∴


∴
考查方向
求数列的前N项和
解题思路
分别表示出S1,S2,的表达,然后找寻规律,求数列的和
易错点
计算能力弱,对数列的相关定理公式掌握不好
教师点评
求解此类问题,关键在于求数列的前N项和时所选用的方法
已知抛物线C的标准方程为

23.求抛物线C的标准方程;
24.记
正确答案
详见解析
解析
由题意,

抛物线C的标准方程为
考查方向
求抛物线的标准方程
解题思路
根据已知条件建立方程,进而求出参数值,求出抛物线的方程
易错点
计算能力弱,相关公式记忆不准确
正确答案
详见解析
解析
设







(ⅰ)


又

不论a取何值,t均与m有关, 即
(ⅱ)







考查方向
直线和圆锥曲线的交汇问题,新概念定义的和圆锥曲线结合题
解题思路
根据稳定点的定义,结合已知条件和抛物线的性质。联立方程组,求解参数,得到答案
易错点
计算能力弱,分类讨论思想运用不好
如图,在四棱锥





19.求证:AB∥EF;
20.若


正确答案
详见解析
解析
∵底面














考查方向
空间几何体中的线线平行的证明
解题思路
根据线面平行证明线线平行
易错点
空间感不全,证明思维混乱
正确答案
详见解析
解析
取



∵






































∵



∵



考查方向
利用空间直角坐标系下的空间向量求二面角的余弦值
解题思路
建立适当的空间直角坐标系,根据空间向量的运算规律求解
易错点
计算能力弱,空间感不强
已知函数
25.当

26.当


正确答案
详见解析
解析
令



故
考查方向
利用导数证明不等式,导数和函数相结合问题
解题思路
先求导,然后判断函数的单调性,构造恰当的函数,证明不等式
易错点
不能正确的构造出函数,求导错误
正确答案
详见解析
解析
当


当

所以

令
令
当

令




因此


所以,当

当

令




因此,


所以,当

综上,当



考查方向
利用导数证明不等式,导数和函数相结合问题
已知不等式成立求参数的取值范围
解题思路
求导,分类讨论,然后判断函数单调性
根据不等式成立,求参数的取值范围
易错点
计算能力弱,分类讨论有重复或有遗漏
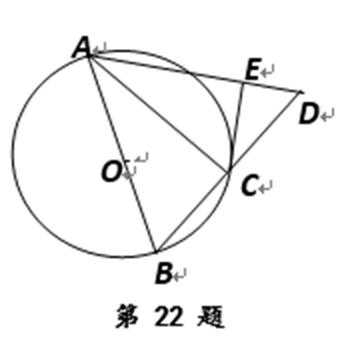
选修4-1:几何证明选讲
如图,AB是圆O的直径,点C在圆O上,延长BC到D使
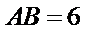
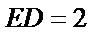
27.求证: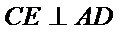
28.求BC的长.
正确答案
详见解析
解析
连接
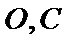
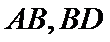

又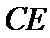
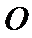
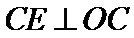
考查方向
圆切线的判定与性质
解题思路
作出半径,然后证明垂直关系
易错点
几何关系找不全,逻辑混乱
正确答案
详见解析
解析
依题意易知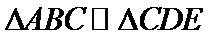
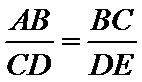
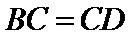
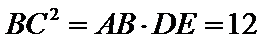
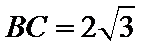
考查方向
与圆有关的比例线段,相似三角形的性质和判定
解题思路
根据圆的比例线段关系,证明三角形相似,然后求出比例等式,进而求出线段的值
易错点
几何关系找不全,逻辑关系混乱
15.已知边长为




正确答案
解析
如图1,取BD的中点E,连AE,CE,由已知条件,面ACE垂直于面BCD,则外接球球新在面ACE内,如图2,OG垂直CE,OE垂直平分AC,其中CG=2GE,角CEA=120度,所以R=OC=OA=
所以外接球的表面积为
考查方向
四面体的结构特征,球的表面积和体积
解题思路
根据题意,求出四面体的外接球的半径,进而求出外接球的表面积
易错点
立体感不强,找不到二面角
知识点
14.x,y满足约束条件

正确答案
解析
如图,约束条件对应的可行域为:
三角形BCD所围成的阴影部分,则目标函数对应的范围为
0~8
考查方向
线性规划
解题思路
根据约束条件作出可行域,然后找到边界值点,求出取值范围
易错点
作图错误,选范围错误
知识点
16.在


正确答案
解析



所以
考查方向
解三角形,正弦定理
解题思路
先求出sinA和sinC的表达式,然后由正弦定理得到sinB的值
易错点
三角函数相关公式掌握不牢固
知识点
13.已知向量


正确答案
解析
由定义可知,
所以此题填
考查方向
平面向量的投影
解题思路
按照投影的计算公式计算
易错点
对投影的概念掌握不牢