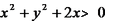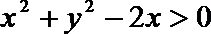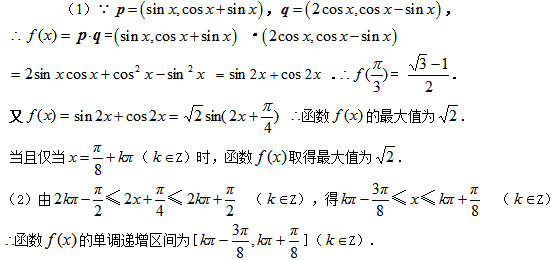- 真题试卷
- 模拟试卷
- 预测试卷
5.已知数列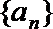
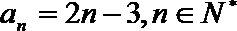
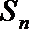
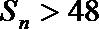
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 如果x、y满足
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.若
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.在




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.下图中,阴影部分的面积是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.现要给四棱锥
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设全集



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.抛物线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.4张卡片上分别写有数字1,2,3,4,从这4张卡片中随机抽取2张,则取出的2张卡片上的数字之和为奇数的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知一几何体的三视图如下,正视图和侧视图都是矩形,俯视图为正方形,在该几何体上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,这些几何形体是( )(写出所有正确结论的编号)。
①矩形;
②不是矩形的平行四边形;
③有三个面为直角三角形,有一个面为等腰三角形的四面体;
④每个面都是等腰三角形的四面体;
⑤每个面都是直角三角形的四面体。
正确答案
①③④⑤
解析
解析已在路上飞奔,马上就到!
知识点
13.如图,是一程序框图,则输出结果为( )。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.设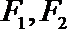
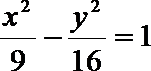
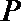
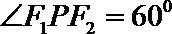

正确答案
16
解析
解析已在路上飞奔,马上就到!
知识点
12.一个公司共有1 000名员工,下设一些部门,要采用分层抽样方法从全体员工中抽取一个容量为50的样本,已知某部门有200名员工,那么从该部门抽取的工人数是( )。
正确答案
10
解析
解析已在路上飞奔,马上就到!
知识点
11.复数
正确答案
-1
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知正数数列



(Ⅰ)求
(Ⅱ)求证

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.(本题有三个小题,请任选两题作答,如果全做,则按前两题计分)
(1)在直角坐标系中,△OAB的顶点坐标O(0 , 0),A(2,0),B(1,
△OAB在矩阵MN的作用下变换所得到的图形的面积,其中矩阵M =

(2)过点P(-3,0)且倾斜角为30°的直线和曲线
(3)证明不等式:
正确答案
答案已在路上飞奔,马上就到!
解析
知识点
17.如图:PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成角是30°,点F是PB的中点,点E在边BC上移动。
(Ⅰ)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;

(Ⅲ)当BE等于何值时,二面角P-DE-A的大小为45°。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 设函数f(x)=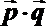
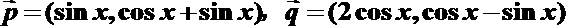
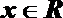
(1)求f(
(2)求函数f(x)的单调递增区间。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知双曲线



(Ⅰ)如果椭圆

(Ⅱ)如果椭圆




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数




(Ⅰ)求a的值;
(Ⅱ)是否存在k的值,使直线
(Ⅲ)如果对于所有

正确答案
解析
解析已在路上飞奔,马上就到!