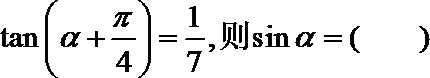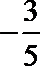- 真题试卷
- 模拟试卷
- 预测试卷
3.等差数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若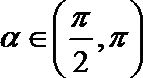
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.设
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 若全集为实数集


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.非零向量

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若实数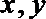
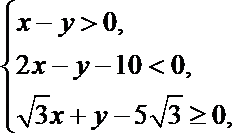
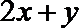
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.如图,函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.在

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.下列命题中,正确的是______________
(1)平面向量




(2)已知
(3)





正确答案
(1)(2)(3)
解析
解析已在路上飞奔,马上就到!
知识点
15.



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.设函数
(1)求
(2)求
正确答案
(1)

(2)由
所以

解析
解析已在路上飞奔,马上就到!
知识点
18.在
(1)若三边长构成公差为4的等差数列,求
(2)已知



正确答案
(1)

由余弦定理:
即
所以
(2)
因为
所以
解析
解析已在路上飞奔,马上就到!
知识点
20.已知

(Ⅰ)求
(Ⅱ)当

正确答案
(Ⅰ)解:
由已知得

当


所以
(Ⅱ)证明:由(Ⅰ)知,

当



当



所以在区间


又

所以在区间


对于

所以
解析
解析已在路上飞奔,马上就到!
知识点
21.已知



(1)求数列
(2)设数列


正确答案
(1)
(2)设
=
因为 
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数
(1)求
(2)如果当



正确答案
(1)定义域为
设
① 当


所以

② 当

所以

③ 当

令


所以



(2)

设
① 当


若

若

所以,当
② 当


所以
综上,实数

解法二 :
设
令

所以

由洛必达法则
所以
解析
解析已在路上飞奔,马上就到!
知识点
19.数列



(I)求证:数列
(II)设
正确答案
(I)令
(2)-(1) :

(II)


① -②
所以
解析
解析已在路上飞奔,马上就到!