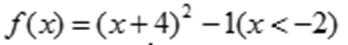- 真题试卷
- 模拟试卷
- 预测试卷
2.

正确答案
6
解析
解析已在路上飞奔,马上就到!
知识点
4.已知定义在R上的函数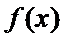
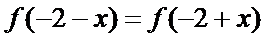
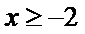
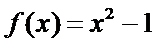
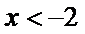
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知奇函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知


正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
11.已知函数
①
②当


③若


④

其中正确命题的序号是_________。
正确答案
③
解析
解析已在路上飞奔,马上就到!
知识点
1.集合



正确答案
[-2,2]
解析
解析已在路上飞奔,马上就到!
知识点
3.设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若关于


正确答案
[1,5/4]
解析
解析已在路上飞奔,马上就到!
知识点
8.二次函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.定义域为




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有点数1、2、3、4、5、6),骰子朝上的面的点数分别为X、Y,则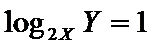
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.函数



①
②对任意

③ 
④若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.若对于任意实数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.设函数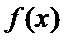
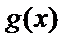
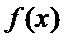
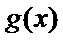
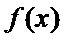
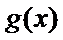
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. (1)已知函数



(2)已知函数


正确答案
(1)设
则当
有
而此时
∴
又∵

但由
得

∴
(2)
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数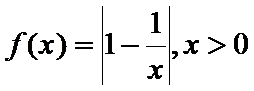
(1)当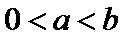
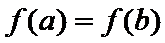

(2)是否存在实数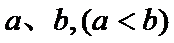
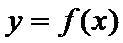
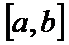
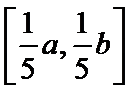
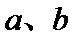
正确答案
(1)证明: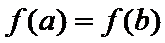
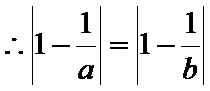
情况1: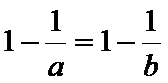
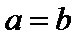
与条件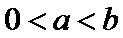
情况2: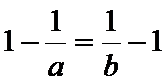
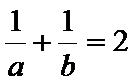
又因为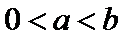
所以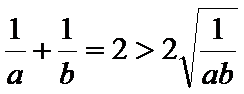
所以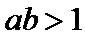
(2)情况1: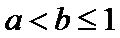
函数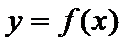
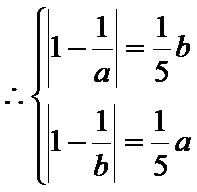
即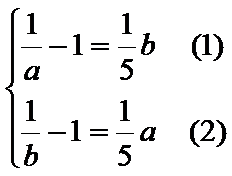
(1)-(2)得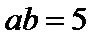
与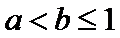
情况2: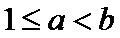
函数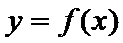
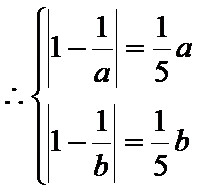
即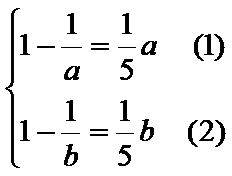
得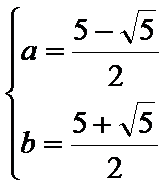
情况3: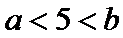
函数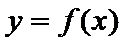

所以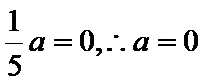
综上,存在实数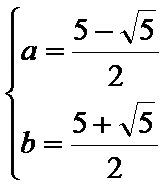
使得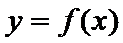
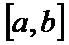
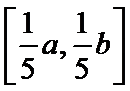
解析
解析已在路上飞奔,马上就到!
知识点
22.对定义在


① 对任意的

② 当

已知函数


(1)试问函数

(2)若函数


(3)在(2)的条件下,讨论方程
正确答案
(1) 当

当

(2)若
不满足①,所以不是
若

在

满足①
由

即
因为
所以 



当

综合上述:
(3)根据(2)知: A=1,
考虑定义域,
方程为 
令
由图形可知:
当
当
当
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数


正确答案

解析
解析已在路上飞奔,马上就到!
知识点
20.设

(1)当

(2)若已知


(3)当


正确答案
(1)减函数
(2)
即
对任意实数
化简整理得
这是关于
所以

(3)
因为
所以
从而
而

所以对任何实数

解析
解析已在路上飞奔,马上就到!
知识点
19. 随着机构改革工作的深入进行,各单位要减员增效,有一家公司现有职员



正确答案
设裁员x (
当
当
答:当 70


当
解析
解析已在路上飞奔,马上就到!