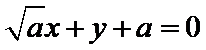- 真题试卷
- 模拟试卷
- 预测试卷
1.设复数z满足

正确答案
解析
由



考查方向
解题思路
复数题也是每年高考必考内容,一般以客观题形式出现,属得分题.高考中复数考查频率较高的内容有:复数的几何意义,共轭复数,复数的模及复数的乘除运算,这类问题一般难度不大,但容易出现运算错误,特别是
易错点
列方程时注意实部、虚部对照,在变形时易错
知识点
4.投篮测试中,每人投3次,至少投中2次才能通过测试。已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为( )
正确答案
解析
根据独立重复试验公式得,该同学通过测试的概率为
考查方向
解题思路
本题首先读懂题意,明白通过测试有两种情况,一是三次命中两次,零一种是三次全部命中,根据独立重复试验公式即可得结果。
易错点
本题主要考查独立重复试验的概率公式与互斥事件和概率公式,分类时易错.
知识点
5.已知M(




正确答案
解析
由题知




解得
考查方向
解题思路
设M在双曲线的上,结合其函数图象和双曲线的性质和向量关系的到
易错点
容易将双曲线与椭圆性质混淆.
知识点
6.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺。问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有( )
正确答案
解析
设圆锥底面半径为r,则




考查方向
解题思路
可以先算出半径,然后算出体积,最后计算堆放斛的米约多少.
易错点
本题主要考查圆锥的性质与圆锥的体积公式,本题易在
知识点
7.设


正确答案
解析
由题知
=
考查方向
解题思路
本题考查平面向量的基本定理,具体解题步骤如下:1.在三角形ABD中用向量加法的三角形法则。2.不断把向量用基底表示.
易错点
本题易在向量的表示过程中出现错误。
知识点
8.函数


正确答案
解析
由五点作图知,











考查方向
解题思路
本题考查了三角函数求解析式的问题,可以列方程组求出
易错点
本题易在计算
知识点
9.执行右面的程序框图,如果输入的t=0.01,则输出的n=( )
正确答案
解析
执行第1次,t=0.01,S=1,n=0,m=

执行第2次,S=S-m=0.25,
执行第3次,S=S-m=0.125,
执行第4次,S=S-m=0.0625,
执行第5次,S=S-m=0.03125,
执行第6次,S=S-m=0.015625,
执行第7次,S=S-m=0.0078125,
考查方向
解题思路
由循环结构的特点,先判断,再执行,分别计算出当前的,s,t的值,即可得到n的值.
易错点
判断框的结构原理
知识点
2.
正确答案
解析
原式=


考查方向
易错点
本题主要考查诱导公式与两角和与差的正余弦公式列在应用公式变形时容易出错。【解题思路】三角函数公式题也是每年高考必考内容,一般以客观题形式出现,属得分题.本题需要把公式进行变形,变得与两角和的正弦公式即可。
知识点
3.设命题


正确答案
解析


考查方向
解题思路
在特称命题否定为全称命题时要注意,


易错点
本题易在特称、全称命题的转化过程中出错.
知识点
10.

正确答案
解析
在




考查方向
解题思路
本题利用排列组合求多项展开式式某一项的系数,试题形式新颖,是中档题,求多项展开式式某一项的系数问题,先分析该项的构成,结合所给多项式,分析如何得到该项,再利用排列组知识求解.
易错点
本题在用三项式的5次展开式易错。
知识点
11.圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16 + 20
正确答案
解析
由正视图和俯视图知,该几何体是半球与半个圆柱的组合体,圆柱的半径与球的半径都为r,圆柱的高为2r,其表面积为


考查方向
解题思路
由于三视图能有效的考查学生的空间想象能力,所以以三视图为载体的立体几何题基本上是高考每年必考内容,高考试题中三视图一般常与几何体的表面积与体积交汇.由三视图还原出原几何体,是解决此类问题的关键.
易错点
本题是三视图问题,主要是简单组合体,必须通过三视图看出直观图。
知识点
12.设函数





正确答案
解析
设





因为







当








考查方向
解题思路
本题主要通过利用导数研究函数的图像与性质解决不等式成立问题。使得

易错点
函数单调性的判断
知识点
某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的宣传费



22.根据散点图判断,

23.根据(I)的判断结果及表中数据,建立y关于x的回归方程;
24.已知这种产品的年利润z与x,y的关系为
(i)当年宣传费
(ii)当年宣传费
附:对于一组数据




正确答案
(Ⅰ)


解析
(Ⅰ)由散点图可以判断,


考查方向
解题思路
试题分析:(Ⅰ)由散点图及所给函数图像即可选出适合作为拟合的函数;
易错点
本题在寻求拟合函数比较易错
正确答案
(Ⅱ)
解析
(Ⅱ)令




∴
∴


∴


考查方向
易错点
在非线性回归方程进行预报预测;应用易错.
正确答案
(Ⅲ)46.24
解析
(Ⅲ)(ⅰ)由(Ⅱ)知,当



(ⅱ)根据(Ⅱ)的结果知,年利润z的预报值

∴当



故宣传费用为46.24千元时,年利润的预报值最大.……12分
考查方向
解题思路
(Ⅲ)(ⅰ)利用



易错点
在非线性回归方程进行预报预测;应用易错.
在直角坐标系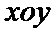
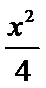
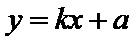
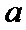
25.当k=0时,分别求C在点M和N处的切线方程;
26.y轴上是否存在点P,使得当k变动时,总有∠OPM=∠OPN?说明理由.
正确答案
(Ⅰ)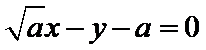
解析
(Ⅰ)由题设可得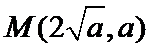
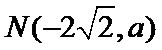
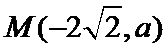
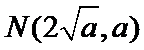
∵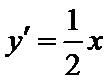
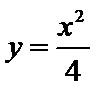
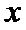
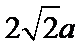
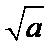
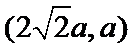
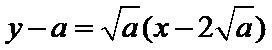
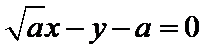
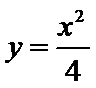
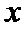
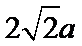
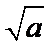
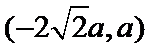
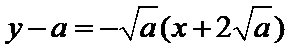
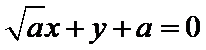
故所求切线方程为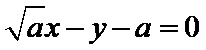
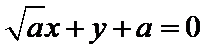
考查方向
解题思路
(Ⅰ)先求出M,N的坐标,再利用导数求出M,N.
易错点
本题在用导数求方程过程中易错
正确答案
(Ⅱ)存在
解析
(Ⅱ)存在符合题意的点,证明如下:
设P(0,b)为复合题意得点,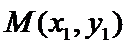
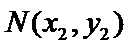
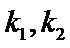
将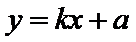
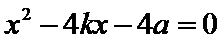
∴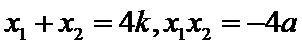
∴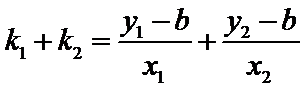
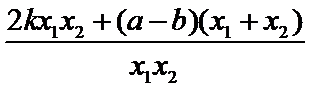
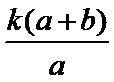
当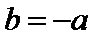
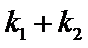
故∠OPM=∠OPN,所以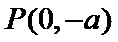
考查方向
解题思路
(Ⅱ)先作出判定,再利用设而不求思想即将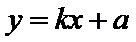
易错点
本题在用导数求方程过程中易错,在直线和曲线的位置关系中易错。






17.求{
18.设


正确答案
(Ⅰ)
解析
(Ⅰ)当



当






所以数列{
所以

考查方向
解题思路
(Ⅰ)先用数列第




易错点
本题在用公式法计算通项公式时n=1易丢.
正确答案
(Ⅱ)
解析
(Ⅱ)由(Ⅰ)知,

所以数列{



解题思路
(Ⅱ)根据(Ⅰ)数列{

易错点
本题在裂项中错出现错误。
如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC.
19.证明:平面AEC⊥平面AFC;
20.求直线AE与直线CF所成角的余弦值.
正确答案
(Ⅰ)(Ⅰ)连接BD,设BD∩AC=G,连接EG,FG,EF,在菱形ABCD中,不妨设GB=1,由∠ABC=120°,可得AG=GC=
由BE⊥平面ABCD,AB=BC可知,AE=EC,
又∵AE⊥EC,∴EG=
在Rt△EBG中,可得BE=

在Rt△FDG中,可得FG=
在直角梯形BDFE中,由BD=2,BE=


∴
∵AC∩FG=G,∴EG⊥平面AFC,
∵EG
解析
见答案
考查方向
解题思路
(Ⅰ)连接BD,设BD∩AC=G,连接EG,FG,EF,在菱形ABCD中,不妨设GB=1易证EG⊥AC,通过计算可证EG⊥FG,根据线面垂直判定定理可知EG⊥平面AFC,由面面垂直判定定理知平面AFC⊥平面AEC;
易错点
本题在证明过程中推理不严密易错。
正确答案
(Ⅱ)
解析
(Ⅱ)如图,以G为坐标原点,分别以












故
所以直线AE与CF所成的角的余弦值为
考查方向
解题思路
(Ⅱ)以G为坐标原点,分别以


易错点
本题在写垂直的过程不能写全条件。
已知函数f(x)=
27.当a为何值时,x轴为曲线
28.用


正确答案
(Ⅰ)
解析
(Ⅰ)设曲线






因此,当


考查方向
解题思路
(Ⅰ)先利用导数的几何意义列出关于切点的方程组,解出切点坐标与对应的
易错点
本题在用切线的斜率易错
正确答案
(Ⅱ)当







解析
(Ⅱ)当


∴
当










当


(ⅰ)若









(ⅱ)若








①若



②若


③若







综上,当







考查方向
解题思路
(Ⅱ)根据对数函数的图像与性质将



易错点
本题在讨论零点的过程中易错。
选修4-1:几何证明选讲
如图,AB是


请回答29-30题
选修4-4:坐标系与参数方程
在直角坐标系






请回答31-32题
选修4—5:不等式选讲
已知函数
请回答33-34题
29.若D为AC的中点,证明:DE是
30.若
31.求

32.若直线






33.当a=1时,求不等式f(x)>1的解集;
34.若f(x)的图像与x轴围成的三角形面积大于6,求a的取值范围.
正确答案
(Ⅰ)详见解析;
解析
(Ⅰ)连结AE,由已知得,AE⊥BC,AC⊥AB,
在Rt△AEC中,由已知得DE=DC,∴∠DEC=∠DCE,
连结OE,∠OBE=∠OEB,
∵∠ACB+∠ABC=90°,∴∠DEC+∠OEB=90°,
∴∠OED=90°,∴DE是圆O的切线.
由已知得DE=DC,∴∠DEC=∠DCE,
连结OE,∠OBE=∠OEB,
∵∠ACB+∠ABC=90°,∴∠DEC+∠OEB=90°,
∴∠OED=90°,∴DE是圆O的切线.
考查方向
解题思路
(Ⅰ)由圆的切线性质及圆周角定理知,AE⊥BC,AC⊥AB,由直角三角形中线性质知DE=DC,OE=OB,利用等量代换可证∠DEC+∠OEB=90°,即∠OED=90°,所以DE是圆O的切线;
易错点
本题在应用与圆有关的线段比例中易错
正确答案
(Ⅱ)60°
考查方向
解题思路
(Ⅱ)设CE=1,由






(Ⅱ)设CE=1,AE=


由射影定理可得,
∴


易错点
本题在应用定理时易错。
正确答案
(Ⅰ)(Ⅰ)
解析
(Ⅰ)因为
∴



考查方向
解题思路
(Ⅰ)用直角坐标方程与极坐标互化公式即可求得

易错点
本题在直角坐标方程与极坐标互化过程中易错。
正确答案
(Ⅱ)
解析
(Ⅱ)将









因为



考查方向
解题思路
(Ⅱ)将将


易错点
本题在求弦长过程中易错。
正确答案
(Ⅰ)
解析
(Ⅰ)当a=1时,不等式
等价于



所以不等式

考查方向
解题思路
利用零点分析法将不等式
易错点
本题在分类讨论是易丢大前提
正确答案
(Ⅱ)(2,+∞)
解析
(Ⅱ)由题设可得,
所以函数





由题设得

所以
考查方向
解题思路
(Ⅱ)将




易错点
在本题在应用函数去绝对值易错。
13.若函数f(x)=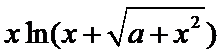
正确答案
1
解析
由题知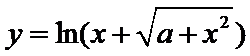
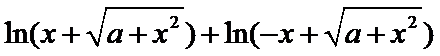
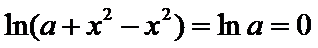
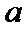
考查方向
解题思路
本题考查了应用函数奇偶性,
易错点
本题易在应用函数奇偶性的过程中易错。函数f(x)=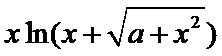
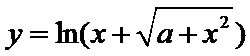
知识点
15.若


正确答案
3
解析
作出可行域如图中阴影部分所示,由斜率的意义知,

考查方向
解题思路
本题考查线性规划,具体解题步骤如下:1、由不等式组画可行域。2、由线性目标函数的几何意义得到其最大值。
易错点
1、本题易在画可行域时发生错误2、本题不容易理解
知识点
16.在平面四边形ABCD中,∠A=∠B=∠C=75°,BC=2,则AB的取值范围是 .
正确答案
(

解析
如图所示,延长BA,CD交于E,平移AD,当A与D重合与E点时,AB最长,在△BCE中,∠B=∠C=75°,∠E=30°,BC=2,由正弦定理可得








考查方向
解题思路
本题可对边进行延长,由正弦定理求出BE然后求出BF,即可得到AB的范围。
易错点
本题在综合应用正余弦定理时易错。
知识点
14.一个圆经过椭圆
正确答案
解析
设圆心为(




考查方向
解题思路
本题考查了椭圆的几何性质,可设出标准式,然后求解。
易错点
本题在设元的过程中易错。