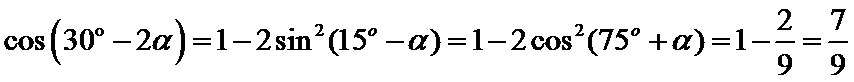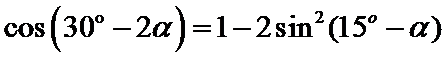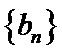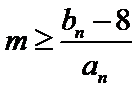理科数学泰安市2016年高三第一次模拟考试

精品

单选题
填空题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共10小题，每小题5分，共50分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

2.已知为实数，则实数t的值为（）

正确答案

解析

，则虚部等于0，

所以

考查方向

本题主要考察了复数代数形式的乘除运算，考察了复数的几何意义，在近几年的高考中经常涉及，难度较小

解题思路

本题属于简单题，可使用直接法，

（1）化简得到的形式

（2）观察实部和虚部，使得虚部等于0

易错点

计算过程易忽略，最后点的判断忽略负号和数是一个整体

知识点

复数的基本概念复数代数形式的混合运算

题型：单选题

分值: 5分

6.已知点及抛物线上一动点，则的最小值是（）

正确答案

解析

如图：注意点Q的位置

根据题意得知

选C

考查方向

本题重点考察了抛物线的标准方程和几何性质，考察了抛物线焦点弦的性质，考察了不等式的应用，借助于数形结合，该题属于简单题

解题思路

1）把转化为点Q到准线的距离问题，

2）利用不等式的性质直接得出结果

易错点

主要易错于的转换

知识点

抛物线的标准方程和几何性质直线、圆及圆锥曲线的交汇问题

题型：单选题

分值: 5分

4.下列结论正确的是（）

A命题“若，则”的否命题为：“若，则”

B已知是R上的可导函数，则“”是“是函数的极值点”的必要不充分条件

C命题“存在，使得”的否定是：“对任意，均有”

DD.命题“角的终边在第一象限角，则是锐角”的逆否命题为真命题

正确答案

解析

根据否命题是条件结论全否，所以A错。

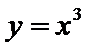
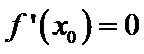
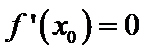
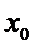
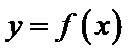
特例中不是函数的极值点，所以则“”是“是函数的极值点”的必要不充分条件正确所以选B

特称命题的否定是全称命题，且否定结论，所以C错

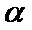
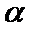
命题“角的终边在第一象限角，则是锐角”是假命题，所以逆否命题为假命题，所以D错所以选B

考查方向

本题主要考察了四种命题及真假判断，导函数的性质，命题的否定，命题的真假判断与应用，充分，必要条件的判定，全（特）称命题的否定，属于基本概念题，使用排除法

解题思路

1）否命题是条件结论全否，命题的否定是只否定结论，对A C D进行选择

2）使用充分，必要条件的判定对BC进行排除

易错点

本题易错于否命题和命题的否定的区别，导致无法排除

知识点

含有逻辑联结词命题的真假判断全（特）称命题的否定

题型：单选题

分值: 5分

5.高为4的直三棱柱被削去一部分后得到一个几何体，它的直观图和三视图中的侧视图、俯视图如图所示，则该几何体的体积是原直三棱柱的体积的（）

正确答案

解析

根据三视图可知直观图为：放倒的四棱锥，

∵底面是直角梯形，且上底为4，下底为2，梯高2

∴

又因为 ∴选C

考查方向

本题重点考察了由三视图还原实物图，考察了棱锥的体积，该题属于简单题

解题思路

1）根据直观图形状：放倒的四棱锥，底面是直角梯形，

2）读取几何图形的数据

易错点

主要出现在两个地方：①不能得到直观图为四棱锥，②直观图读取直观图数据错误，特别是底面上的长宽数据

知识点

由三视图还原实物图

题型：单选题

分值: 5分

8.分别在区间内任取两个实数，则不等式恒成立的概率为（）

正确答案

解析

根据题意作图

基本事件空间区域的面积为

对应的面积

∴ 选B

考查方向

该题主要考察了几何概型，考察了定积分运算，考察了正弦函数的定积分，该题属于简单题

解题思路

该题解题思路

1）题意画出满足条件的区域，以及不等式表示的区域

2）求出矩形区域面积和利用定积分求对应的面积

3）使用几何概型公式计算出概率

易错点

主要易错于几何概型的形式出错，定积分求措

知识点

与面积、体积有关的几何概型

题型：单选题

分值: 5分

1.已知全集，集合，集合，则（）

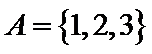
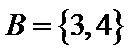
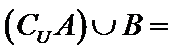
正确答案

解析

使用集合交集的性质，借助数轴容易得出答案C。

考查方向

本题主要考察集合交并补集的混合运算，考察了venn图表达集合的关系及运算，高考选择题中属于常见题，难度较小

解题思路

本题属于简单题，可使用venn图直接观察得出

易错点

直接观察漏解

知识点

交、并、补集的混合运算

题型：单选题

分值: 5分

3.右图是一个程序框图，则输出S的值是（）

A84

B35

C26

D10

正确答案

解析

考查方向

本题主要考察了程序框图，考察了循环结构，框图是在近几年高考中经常出现，考察形式基本不变，难度系数不高，

解题思路

1）写出循环结构，找出S结果的规律

2）根据运算框，累计求和

3）找出跳出循环的位置

易错点

本题易在判断上出错，导致提前或者延后跳出循环，第二没有发现S结果之间的规律，导致出错，

知识点

程序框图

题型：单选题

分值: 5分

7.已知，点满足，则的最大值为（）

正确答案

解析

根据约束条件画出可行域

由图可知在点A（2，2）处取得最值即z=6-5=1 选D

考查方向

该题主要考察了简单的线性规划问题，考察了向量的坐标运算，考察了向量的数量积运算，该题属于简单题

解题思路

该题解题思路

1）题意画出可行域，标记可行域的顶点

2）根据得出

3）通过简单的线性规划问题最优解的性质得出最值

易错点

主要体现在两个方面①可行域不规范，②目标函数转化错误

知识点

不等式的性质其它不等式的解法

题型：单选题

分值: 5分

10.奇函数的定义域为R，若为偶函数，且，则的值为（）

正确答案

解析

考查方向

该题主要考察了函数奇偶性的性质，奇偶函数图象的对称性，函数的周期性，该题属于综合类，比较难

解题思路

该题解题思路

1）为偶函数得出函数关于x=1对称，为奇函数得出关于原点对称

2）根据对称性得出函数为周期函数，周期T=4

3）利用周期性易得取值

易错点

主要易错于为偶函数对应的性质

知识点

函数奇偶性的性质函数的值

题型：单选题

分值: 5分

9.已知函数的图象向右平移个单位后与原图象重合，则的最小值是（）

正确答案

解析

根据平移后与原函数重合可知平移的距离为周期可知

∴选Ａ

考查方向

该题主要考察了函数y=Asin（ωx+φ）的图象变换，考察了三角函数的周期性及其求法，该题属于简单题

解题思路

该题解题思路

1）根据平移后与原函数重合可知平移的距离为周期的整数倍

2）使用周期与的关系建立关系式

3）利用解析式求最值得到结果

易错点

主要易错于无法理解与原图重合对应的含义

知识点

三角函数的周期性及其求法函数y=Asin（ωx+φ）的图象变换三角函数中的恒等变换应用

填空题本大题共5小题，每小题5分，共25分。把答案填写在题中横线上。

题型：填空题

分值: 5分

11.若，则的值为__________.

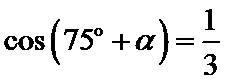
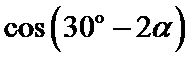
正确答案

解析

考查方向

该题主要考察了二倍角的余弦，运用诱导公式化简求值，比较难

解题思路

该题解题思路

1）使用倍角公式计算

2）使用角之间的关系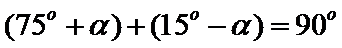两角互余

3）根据诱导公式计算出结果

易错点

主要易错于使用诱导公式的时候正负号的变化

知识点

三角函数的化简求值

题型：填空题

分值: 5分

13.设二项式的展开式中的系数为A，常数项为B，若B=44，则 ▲ .

正确答案

解析

中的通项为，

，.

考查方向

本题主要考察二项式的展开式，高考中经常出现，考察难度不高

解题思路

写出二项展开式，确定r，直接计算

易错点

本题易错在二项展开式记忆错误

知识点

求二项展开式的指定项或指定项的系数

题型：填空题

分值: 5分

14.已知平面向量满足，且的夹角为120°，则的模的取值范围为 ▲ .

正确答案

解析

考查方向

本题主要考察了向量的减法及其几何意义，考察了向量的三角形法则，考察了正弦定理，该题比较综合，属于中档题

解题思路

1）根据题意使用有向线段表示向量，并构造三角形

2）利用三角形的正弦定理得出的模与夹角的关系，

3）根据角的取值范围得到取值范围

易错点

本题易错在无法找到有效的解题思路

知识点

平面向量数量积的运算数量积表示两个向量的夹角

题型：填空题

分值: 5分

15.若函数存在唯一的零点，则实数t的取值范围为 ▲ .

正确答案

解析

∵当x=0时无零点，

考查方向

本题主要考察了导数的加法与减法法则，函数单调性的判断与证明，函数单调性的性质，该题比较综合，属于中档题

解题思路

1）对函数当x=0时进行讨论不成立

2）当

3）讨论进行讨论单调性

4）借助单调性及其最值得出结论

易错点

本题易错在分类不清或者对单调性判断错误

知识点

函数零点的判断和求解

题型：填空题

分值: 5分

12.随机抽取100名年龄在…，年龄段的市民进行问卷调查，由此得到样本的频率分布直方图如图所示，

从不小于30岁的人中按年龄段分层抽样的方法随机抽取22人，则在年龄段抽取的人数为 ▲ .

正确答案

解析

根据频率分布直方图可知

考查方向

本题考察频率分布直方图，分层抽样方法，比较简单

解题思路

本题的解题思路

1）根据小矩形面积对应为频率，计算不小于30岁的频率，与之间的频率。

2）计算两部分的比例

3）使用分层抽样的性质计算人数

易错点

本题易于在分层抽样的性质上出错

知识点

分层抽样方法用样本的频率分布估计总体分布

简答题（综合题）本大题共75分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

17. 一个袋中装有7个大小相同的球，其中红球有4个，编号分别为1，2，3，4；蓝球3个，编号为2，4，6，现从袋中任取3个球（假设取到任一球的可能性相同）.

（I）求取出的3个球中，含有编号为2的球的概率；

（II）记为取到的球中红球的个数，求的分布列和数学期望.

正确答案

见解析

解析

考查方向

本题考察了排列、组合及简单计数问题, 古典概型的概率, 超几何分布, 离散型随机变量及其分布列、均值与方差,该题属于简单题

解题思路

本题的解题思路

1）使用排列组合知识写出基本事件空间和含有编号为2的球个数，并用古典概型的概率公式计算概率

2）分清所有可能取值

3）根据情况依次求概率

4）写分布列以及期望

易错点

本题易错在第一问分类不清，第二问把超几何分布当成二项分布

知识点

随机事件的频率与概率求离散型随机变量的分布列离散型随机变量及其分布列、均值与方差

题型：简答题

分值: 12分

18. 已知等比数列的公比，且成等差数列，数列满足： .

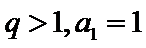
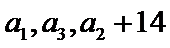
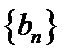
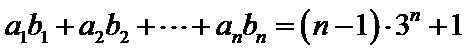
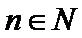
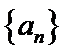
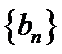
（I）求数列和的通项公式；

（II）若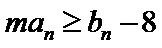恒成立，求实数m的最小值.

正确答案

见解析

解析

考查方向

本题考察了等差、等比数列的基本运算，考察了等比数列的基本运算，考察了由与的关系求通项，考察了函数的恒成立问题，考察了数列的单调性问题。

解题思路

1）借助等差数列性质求出

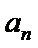
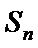
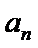
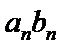
2）利用由与的关系求通项的方法求出并确定

3）对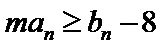移项得到新数列

4）讨论新数列单调性，并求出最值

易错点

本题第一问忽略验证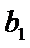，第二问数列的单调性判断不出

知识点

等差数列的性质及应用等比数列的性质及应用

题型：简答题

分值: 12分

19. 如图，在三棱锥中，平面90°，，E是AB的中点，M是CE的中点，N点在PB上，且.

（I）证明：平面平面PAB；

（II）证明：MN//平面PAC；

（III）若，求二面角的大小.

正确答案

见解析

解析

考查方向

本题考察了直线和平面平行的判定定理，考察了面和面垂直的判定定理，考察了面与面之间的位置关系，空间向量的正交分解及其坐标表示，考察了利用空间向量证明平行，考察了用空间向量求平面间的夹角

解题思路

该题解题关键在于找到所求内容的突破点

1）根据平面

2）由线面垂直得到面面垂直

3）取AE的中点，借助中位线由面面平行证明线面平行

4）根据已知条件建立坐标系，并标记所需点的坐标

5）计算相应面的法向量，并求向量的夹角

6）判断两面角的大小确定二面角

易错点

本题容易在辅助线建立过程出错，空间直角坐标系建立及其坐标表示出错，二面角的判断出错

知识点

平面与平面平行的判定与性质平面与平面垂直的判定与性质线面角和二面角的求法

题型：简答题

分值: 13分

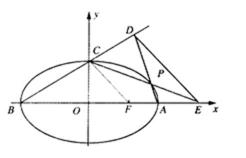
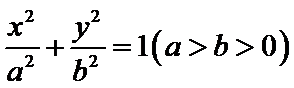
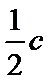
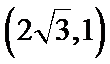
20. 如图：A,B,C是椭圆的顶点，点为椭圆的右焦点，原点O到直线CF的距离为，且椭圆过点.

（I）求椭圆的方程；

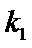
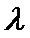
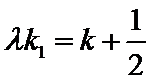
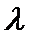
（II）若P是椭圆上除顶点外的任意一点，直线CP交x轴于点E，直线BC与AP相交于点D，连结DE.设直线AP的斜率为k，直线DE的斜率为，问是否存在实数，使得成立，若存在求出的值，若不存在，请说明理由.

正确答案

见解析

解析

考查方向

本题考察了椭圆的定义及标准方程，，考察了圆锥曲线的定点、定值问题，

解题思路

1）点到直线的距离公式得到a,b的关系，根据点在椭圆上联立求出椭圆方程

2）设点p，根据要求求出直线AP，与直线BC求出点D

3）根据直线CP得到点E

4）使用两点间斜率公式得到DE斜率，化简得到结论

易错点

本题主要有以下几个错误：

1）椭圆方程求错

2）找不到有效突破点，导致运算量加大，无法得出理想结果

知识点

椭圆的定义及标准方程椭圆的几何性质直线、圆及圆锥曲线的交汇问题

题型：简答题

分值: 12分

16.已知函数

（I）求函数的单调递减区间；

（II）在中，分别是角A、B、C的对边，，求c.

正确答案

见解析

解析

考查方向

本题主要考察了二倍角的余弦公式，考察了两角和与差的正弦公式，考察了三角函数的恒等变换及化简求值，考察了余弦定理，余弦定理的应用，均值定理，考察了向量的数量积运算

解题思路

该题解题思路如下

1）使用和角公式展开

2）利用倍角公式对解析式降次

3）使用辅助角公式对解析式化简

4）利用特殊角的三角函数求值得到角C，

5）使用余弦定理得到a，b的关系，使用余弦定理求c

易错点

该题易于忽略了对C的范围的判断，该题属于简单

知识点

三角函数的化简求值三角函数中的恒等变换应用

题型：简答题

分值: 14分

21.已知函数

（I）若函数与函数在点处有共同的切线l，求t的值；

（II）证明：；

（III）若不等式对所有的都成立，求实数a的取值范围.

正确答案

见解析

解析

考查方向

本题考察了导函数的几何意义，函数的单调性的判断，考察了函数最值，考察了导数的加法和减法运算，考察了简单复合函数的导函数，考察了函数恒成立问题，考察了函数性质的综合应用，考察了函数的分类讨论思想

解题思路

本题解题思路

1）根据共同的切线的理解得到该点处导函数值与函数值都相等得到t

2）利用单调性确定绝对值内的正负，去掉绝对值号，利用对式子进行证明

3)构造关于m的一次函数，把x当作参数消掉m后再使用恒成立问题的解答得出结果

易错点

本题易错在以下几个方面

1）对共同的切线理解不足，第一问出错

2）不能有效去掉绝对值，使用错的解题思想

3）变量间关系不能有效理清

知识点

函数性质的综合应用导数的运算不等式与函数的综合问题

理科数学 热门试卷

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

理科数学热门试卷