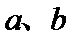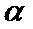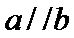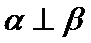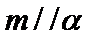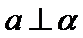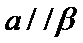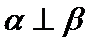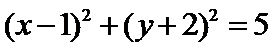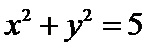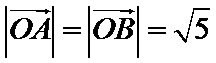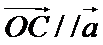- 真题试卷
- 模拟试卷
- 预测试卷
3.若平面向量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若当


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知全集

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知命题

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.设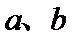
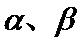
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知正四面体





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.在



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.计算
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.在数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.直线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.如图,










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.某跳小运动员进行





(Ⅰ)求这条抛物线的解析式;
(Ⅱ)该运动员按(Ⅰ)中抛物线运行,要使此次跳水不至于失误,那么运动员在空中调整好入水姿势时,距池边的水平距离至多为多少米?
正确答案
解:(Ⅰ)在给定的直角坐标系下,设最高点为

抛物线的解析式为
由题意知:




所以有

∵抛物线对称轴在

又∵抛物线开口向下,∴

后一组解舍去.∴


∴抛物线的解析式为
(Ⅱ)由题意要使某次跳水不至于失误,那么运动员在空中调整好入水姿势时,距水面高度不小于
则应有

∴运动员此时距池边的距离至多为
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,在直四棱柱







(Ⅰ)求证:
(Ⅱ)求证:
(Ⅲ)求二面角
正确答案
解:(Ⅰ)∵
∴直线


∴


∴
(Ⅱ)
取



∵

∴

∴


又直四棱柱



∴
(Ⅲ)
∵
过点




则
∴

又
∴


解析
解析已在路上飞奔,马上就到!
知识点
19.将圆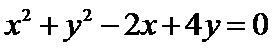
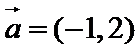
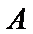
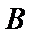
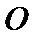
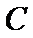
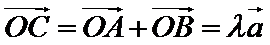
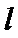
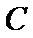
正确答案
解:
将圆的方程
∴圆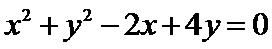

∵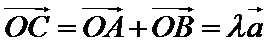
∴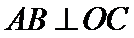
∴直线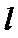

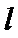
由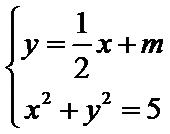

设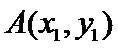
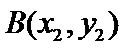
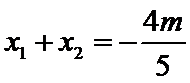
∴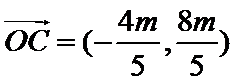
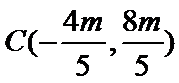
解得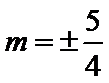
当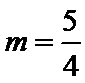
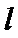
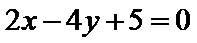
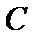

当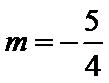
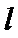
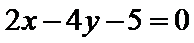
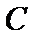
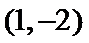
解析
解析已在路上飞奔,马上就到!
知识点
16.如图,





(Ⅰ)若

(Ⅱ)求

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数


(Ⅰ)若


(Ⅱ)若


(Ⅲ)若


正确答案
解:(Ⅰ)
∴


∴

∴
∴

(Ⅱ)由

当

则
∴

∴



(Ⅲ)当

∴

设直线



则
∴
又

∴
∴
方程

则
当


当


∴
又当




∴
∴


∴与曲线


解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列



(Ⅰ)证明数列

(Ⅱ)设




正确答案
证明:(Ⅰ)∵

∴
∴

(Ⅱ)
∴当
解析
解析已在路上飞奔,马上就到!