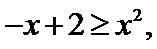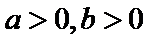- 真题试卷
- 模拟试卷
- 预测试卷
3.已知命题p: ∀x

正确答案
解析
“

故命题p: ∀x



知识点
6.设等差数列{an}的前n项和为




正确答案
解析
由





知识点
7.已知函数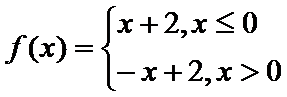
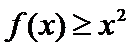
正确答案
解析
当

解得
当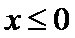
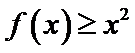
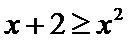
解得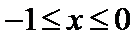
故不等式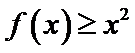
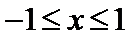
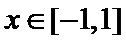
知识点
9.函数











正确答案
解析
由

由

得

因为

所以

知识点
4.设

正确答案
解析
因为




知识点
2.复数
正确答案
解析

知识点
1.若集合


正确答案
解析






知识点
8.设


正确答案
解析
因为


故
故


知识点
10.已知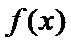
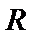
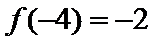

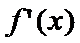
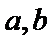
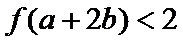
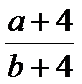
正确答案
解析
因为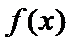

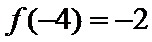
所以
由导函数的图象可知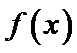
由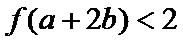
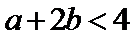
根据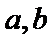
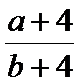


而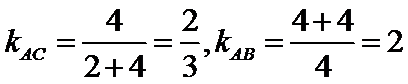

知识点
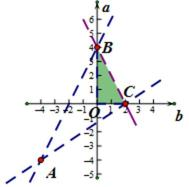
5.设


正确答案
解析
如图,为矩形.
设









两条平行直线,其中一条垂直一个平面,那么另一条也垂直于这个平面,故B正确;
对于C,设









对于D,设









知识点
11.函数
正确答案
解析
要使


知识点
13.中央电视台1套连续播放5个广告,其中3个不同的商业广告和2个不同的公益宣传广告,要求最后播放的必须是公益宣传广告,且2个公益宣传广告不能连续播放,则不同的播放方式有 _____ 种(用数字作答)。
正确答案
36
解析
最后一个播放公益广告有



知识点
15.下面关于
①


②若



③设函数




④函数






其中正确的判断是__________(把你认为正确的判断都填上)
正确答案
①②④
解析
因为函数


对于②,用




对于③,因为






对于④,存在



知识点
12.程序框图(即算法流程图)如图所示,其输出结果是_________
正确答案
31
解析
根据流程线依次执行,

知识点
14.


正确答案
6
解析
由题意知在


而
所以
解得
而当


知识点
18.已知函数

(Ⅰ)求函数
(Ⅱ)设











正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.如图,在四棱锥


(Ⅰ)证明 
(Ⅱ)求EB与底面ABCD所成的角的正切值.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.定义在





(Ⅰ)求证:
(Ⅱ)求证:对任意的

(Ⅲ)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(Ⅰ)若

(Ⅱ)若


(Ⅲ)设函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.一个袋中装有大小相同的球10个,其中红球8个,黑球2个,现从袋中有放回地取球,每次随机取1个. 求:
(Ⅰ)连续取两次都是红球的概率;
(Ⅱ)如果取出黑球,则取球终止,否则继续取球,直到取出黑球,取球次数最多不超过4次,求取球次数
正确答案
解析
解析已在路上飞奔,马上就到!