- 真题试卷
- 模拟试卷
- 预测试卷
1.等差数列{an}中,a4=1,a6+a10=16,则a12=________
正确答案
15
解析
解析已在路上飞奔,马上就到!
知识点
2.集合I={-3,-2,-1,0,1,2},A={-1,1,2},B={-2,-1,0},则A
正确答案
{-3,-1,1,2}
解析
解析已在路上飞奔,马上就到!
知识点
6.已知:0<









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数f(x)=log2(x2-ax+3a)在[2,+∞
正确答案
-4<a≤4
解析
解析已在路上飞奔,马上就到!
知识点
9.若函数y=f(x)的图象与函数g(x)=(
正确答案
-3
解析
解析已在路上飞奔,马上就到!
知识点
10.若函数f(x)=loga(x+
正确答案
(0,1)
解析
解析已在路上飞奔,马上就到!
知识点
3.函数f(x)=sin(

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.函数f(x)=


正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
4.函数f(x)是奇函数,g(x)是偶函数且f(x)+g(x)=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数f(x)=2sin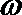
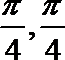
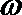
正确答案
-2≤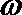
解析
解析已在路上飞奔,马上就到!
知识点
11.函数f(x)=
正确答案
[0,1
解析
解析已在路上飞奔,马上就到!
知识点
13.已知f(3x)=4xlog23+1,则
正确答案
230
解析
解析已在路上飞奔,马上就到!
知识点
14.函数f(x)=2x,对x1,x2∈R+,x1≠x2,




正确答案
<
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数f(x)=
正确答案
(-∞,
解析
解析已在路上飞奔,马上就到!
知识点
16.已知数列{xn}的首项x1=3,通项
(1)求p、q的值;
(2){xn}前n项和为Sn,计算S10的值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设数列{an}的前n项和Sn=2an-2n(n∈N+)。
(1)求a2、a3的值;
(2)证明
(3)求Sn关于n的表达式。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数f(x)=x2+alnx(a为常数)。
(1)若a=-4,讨论f(x)的单调性;
(2)若a≥-4,求f(x)在[1,e]上的最小值及相应的x的值;
(3)若对任意x∈[1,e],f(x)≤(a+2)x都成立,求实数a的取值范围。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.函数f(x)=x3-3ax2+3bx的图象与直线12x+y-1=0相切于点(1,-11)
(1)求a、b的值;
(2)方程f(x)=c有三个不同的实数解,求c的取值范围。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数f(x)=2sin2(



(1)求f(x)的最大值和最小值;
(2)若存在x∈[

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.设函数f(x)=ax2+8x+3(a<0),对于给定的负实数a,有一个最大正数
x∈[0,
(1)当a=-2时,求
(2)a为何值时,
正确答案
解析
解析已在路上飞奔,马上就到!










