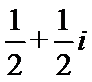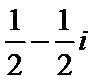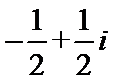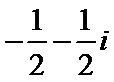- 真题试卷
- 模拟试卷
- 预测试卷
1.已知全集



正确答案
解析
由于P中含1、2、3、4、6,Q中含有1、2、3,而没有4、6,所以求

知识点
7.函数
正确答案
解析
显然这是一个偶函数.当

知识点
8.某教师一天上3个班级的课,每班一节,如果一天共9节课,上午5节、下午4节,并且教师不能连上3节课(第5和第6节不算连上),那么这位教师一天的课的所有排法有( )
正确答案
解析
从9节课中任选3节来排共有
其中3节连上的有

知识点
10.函数














正确答案
解析
由题意得,

当

当


只需


知识点
2.复数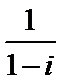
正确答案
解析
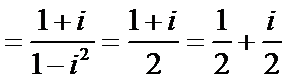
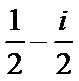
知识点
3.下列命题中错误的是( )
正确答案
解析
A显然正确;
对B:若

若

所以

知识点
4.将函数


正确答案
解析
当


得
当


得
故选B.
知识点
5.已知命题





正确答案
解析
函数
函数

所以直线
知识点
6.R上的奇函数




正确答案
解析
据题意得,这是一个周期为3的周期函数,且为奇函数.所以
知识点
9.如图,菱形






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.函数
正确答案
-2
解析
求导得:


知识点
12.设




正确答案
4
解析


由


注意B只是
知识点
14.设










①设



②若




③对


④设




其中的真命题是___________.(写出所有真命题的编号)
正确答案
①③④
解析
①在


②因为

③因为

④在


知识点
13.在△ABC中,


正确答案
解析
由面积相等得:
由余弦定理得:
知识点
15.函数


(1)求函数
(2)设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.某市职教中心组织厨师技能大赛,大赛依次设基本功(初赛)、面点制作(复赛)、热菜烹制(决赛)三个轮次的比赛,已知某选手通过初赛、复赛、决赛的概率分别是


(I)设该选手参赛的轮次为

(Ⅱ)对于(I)中的

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数


(I)求函数
(II)设函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.
(1)求
(2)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.设函数



(1)求证:
(2)试问:在


(3)解关于x的不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(Ⅰ)求函数
(Ⅱ)求证:
(Ⅲ)对于函数













正确答案
解析
解析已在路上飞奔,马上就到!