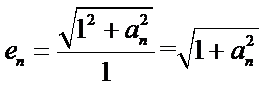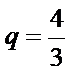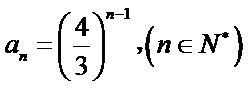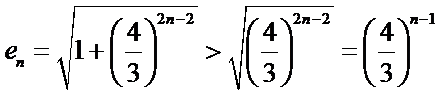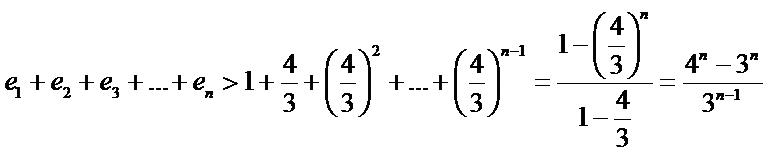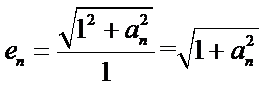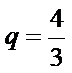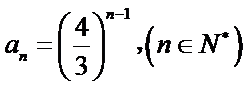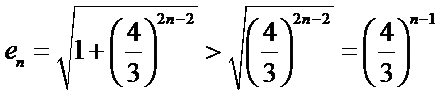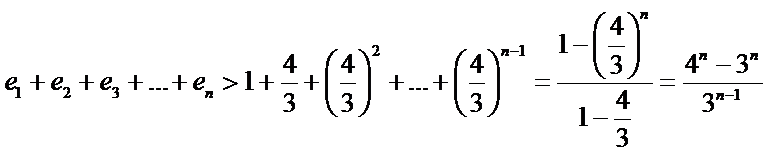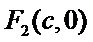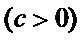- 真题试卷
- 模拟试卷
- 预测试卷
1.设集合

正确答案
解析
由题意,
考查方向
解题思路
集合的概念及运算一直是高考的热点,几乎是每年必考内容,属于容易题.一般是结合不等式,函数的定义域值域考查,解题的关键是结合韦恩图或数轴解答
易错点
本题易在进行交集运算时发生错误。
知识点
5.某公司为激励创新,计划逐年加大研发资金投入.若该公司2015年全年投入研发资金130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是()
(参考数据:lg 1.12≈0.05,lg 1.3≈0.11,lg2≈0.30)
正确答案
解析
设第





考查方向
解题思路
本题考查等比数列的实际应用.在实际问题中平均增长率问题可以看作是等比数列的应用,解题时要注意把哪个作为数列的首项,然后根据等比数列的通项公式写出通项,列出不等式或方程就可解得结论.
易错点
本题考查等比数列的实际应用.在解指数型不等式时,不清楚两边同取对数的技巧。
知识点
6.秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为3,2,判断出v的值为()
正确答案
解析
初始值








考查方向
解题思路
是高考的热点之一,几乎是每年必考内容,多半是考循环结构,基本方法是将每次循环的结果一一列举
易错点
本题在循环过程中写的不全面
知识点
9.设直线l1,l2分别是函数f(x)= 
正确答案
解析
由题设知:不妨设




得:





又



我们写出





此时点



①、②两式联立可解得交点


当且仅当

而

考查方向
解题思路
本题首先考查导数的几何意义,其次考查最值问题,解题时可设出切点坐标,利用切线垂直求出这两点的关系,同时得出切线方程,从而得点


易错点
本题首先考查导数的几何意义,容易在用导数后发生错误。
知识点
2.设i为虚数单位,则
正确答案
解析
二项式


考查方向
解题思路
本题考查二项式定理及复数的运算,复数的概念及运算也是高考的热点,几乎是每年必考内容




易错点
本题考查二项式定理及复数的运算,在用二项式的通项时,易把r+1项看成r项
知识点
3.为了得到函数

正确答案
解析
试题分析:由题意,为了得到函数


考查方向
解题思路
本题考查三角函数的图象平移,在函数











易错点
本题考查三角函数的图象平移的问题,本题容易在平移前,平移后的曲线混淆
知识点
4.用数字1,2,3,4,5组成没有重复数字的五位数,其中奇数的个数为()
正确答案
解析
由题意,要组成没有重复的五位奇数,个位数为1、3、5中的一个,其它位置随意排列有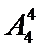
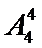
考查方向
解题思路
利用排列组合计数时,关键是正确进行分类和分步,分类时要注意不重不漏,分步时要注意整个事件的完成步骤.在本题中,个位是特殊位置,第一步应先安排这个位置,第二步再安排其他四个位置
易错点
本题考查排列组合问题,容易在分类和分布中发生问题
知识点
7.设p:实数x,y满足(x–1)2–(y–1)2≤2,q:实数x,y满足
正确答案
解析
画出可行域,可知命题q中不等式组表示的平面区域
考查方向
解题思路
本题考查充分性与必要性的判断问题,首先是分清条件和结论,然后考察条件推结论,结论推条件是否成立.这类问题往往与函数、三角、不等式等数学知识结合起来考,本题条件与
易错点
本题考查充分性与必要性的判断问题,条件和结论的区分上易混淆。
知识点
8.设O为坐标原点,P是以F为焦点的抛物线


正确答案
解析








考查方向
解题思路
本题考查抛物线的性质,结合题意要求,利用抛物线的参数方程表示出抛物线上点



易错点
本题考查抛物线的性质,用基本不等式时易错
知识点
10.在平面内,定点A,B,C,D满足












正确答案
解析
由题意,






同理可得,






所以正三角形

我们以



由



而


可以写出
则
当


考查方向
解题思路
本题考查平面向量的数量积与向量的模,由于结论是要求向量模的平方的最大值,因此我们要把它用一个参数表示出来,解题时首先对条件进行化简变形,本题中得出




易错点
本题考查平面向量的数量积与向量的模,在求向量模的平方的最大值易错
知识点
15.在平面直角坐标系中,当P(x,y)不是原点时,定义P的“伴随点”为
当P是原点时,定义P的“伴随点“为它自身,平面曲线C上所有点的“伴随点”所构成的曲线
①若点A的“伴随点”是点

②单位圆的“伴随曲线”是它自身;
③若曲线C关于x轴对称,则其“伴随曲线”
④一条直线的“伴随曲线”是一条直线.
其中的真命题是_____________(写出所有真命题的序列).
正确答案
②③
解析
① 设





























随点分别是














考查方向
解题思路
本题考查新定义问题,属于创新题,符合新高考的走向.它考查学生的阅读理解能力,接受新思维的能力,考查学生分析问题与解决问题的能力,新定义的概念实质上只是一个载体,解决新问题时,只要通过这个载体把问题转化为我们已经熟悉的知识即可.本题新概念“伴随”实质是一个变换,一个坐标变换,只要根据这个变换得出新的点的坐标,然后判断,问题就得以解决.
易错点
本题考查新定义问题,属于创新题,易在定义的分析和对称性的应用中出错。
知识点
11.cos2

正确答案
解析
由二倍角公式得
考查方向
解题思路
这是一个来自于课本的题,直接利用课本公式解题,这告诉我们一定要立足于课本.有许多

易错点
本题考查了三角函数二倍角公式,二倍角公式的记忆可能发生错误
知识点
12.同时抛掷两枚质地均匀的硬币,当至少有一枚硬币正面向上时,就说这次试验成功,则在2次试验中成功次数X的均值是 .
正确答案
解析
由题可知,
在一次试验中,试验成功(即至少有一枚硬币正面向上)的概率为
∵ 2次独立试验成功次数

考查方向
解题思路
本题考查随机变量的均值(期望),根据期望公式,首先求出随机变量的所有可能取值


易错点
本题考查随机变量的均值(期望),易在公式记忆和应用中出错。
知识点
13.已知三棱镜的四个面都是腰长为2的等腰三角形,该三棱锥的正视图如图所示,则该三棱锥的体积是 。
正确答案
解析
由题可知,∵三棱锥每个面都是腰为2的等腰三角形,由正视图可得如下俯视图,且三棱锥高为
考查方向
解题思路
本题考查三视图,考查几何体体积,考查学生的识图能力.解题时要求我们根据三视图想象出几何体的形状,由三视图得出几何体的尺寸,为此我们必须掌握基本几何体(柱、锥、台、球)的三视图以及各种组合体的三视图.
易错点
本题考查三视图,考查几何体体积,考查学生的识图能力.在识图时易错。
知识点
14.已知函数f(x)是定义在R上的周期为2的奇函数,当0<x<1时,f(x)=,则f()+ f(1)= 。
正确答案
解析
首先,

而

所以:

又

故
考查方向
解题思路
【名师点睛】本题考查函数的奇偶性,周期性,属于基本题,在求值时,只要把


易错点
本题考查函数的奇偶性,周期性,易在奇偶性的应用中发生错误
知识点
如图,在四棱锥P-ABCD中,AD∥BC,


21.在平面PAB内找一点M,使得直线CM∥平面PBE,并说明理由;
22.若二面角P-CD-A的大小为45°,求直线PA与平面PCE所成角的正弦值.
正确答案
(Ⅰ)在梯形ABCD中,AB与CD不平行.
延长AB,DC,相交于点M(M∈平面PAB),点M即为所求的一个点.理由如下:

所以四边形BCDE是平行四边形.
从而CM∥EB.
又EB

所以CM∥平面PBE.
解析
(I)延长


∵

∴
∵
∴
∵

∴四边形

∵
∴
∴
∵

∴

∵


∴





解题思路
本题考查线面平行、线线平行、向量法等基础知识,考查空间想象能力、分析问题的能力、计算能力.
易错点
本题考查线面平行、线线平行、向量法等基础知识,考查空间想象能力、分析问题的能力、计算能力.本题易在第一问找点时出错.
正确答案
(Ⅱ)
解析
(Ⅱ)由已知,CD⊥PA,CD⊥AD,PA
所以CD⊥平面PAD.
从而CD⊥PD.
所以
所以
设BC=1,则在Rt△PAD中,PA=AD=2.
过点A作AH⊥CE,交CE的延长线于点H,连接PH.
易知PA⊥平面ABCD,
从而PA⊥CE.
于是CE⊥平面PAH.
所以平面PCE⊥平面PAH.
过A作AQ⊥PH于Q,则AQ⊥平面PCE.
所以
在Rt△AEH中,
所以AH=
在Rt△PAH中,PH=

所以sin


解题思路
本题考查线面平行、线线平行、向量法等基础知识,考查空间想象能力、分析问题的能力、计算能力.
易错点
本题考查线面平行、线线平行、向量法等基础知识,考查空间想象能力、分析问题的能力、计算能力.本题易在第一问找点时出错.
已知数列{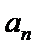
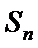
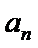
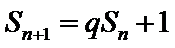
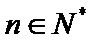
23.若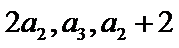
24.设双曲线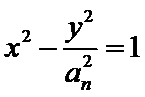
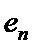
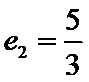
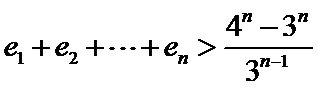
正确答案
(Ⅰ)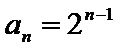
解析
(Ⅰ)由已知,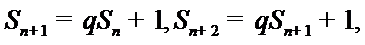
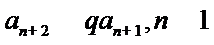
又由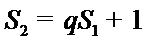
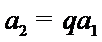
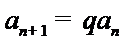
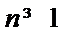
所以,数列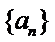
从而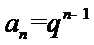
由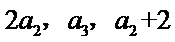
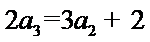
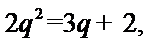
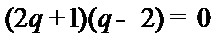
由已知,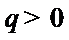
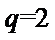
所以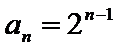
考查方向
解题思路
本题考查数列的通项公式、双曲线的离心率、等比数列的求和公式等基础知识,考查学生的分析问题解决问题的能力、计算能力.在第(Ⅰ)问中,已知的是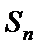
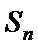
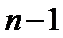
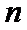
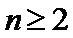
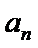
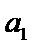
易错点
本题考查数列的通项公式、双曲线的离心率、等比数列的求和公式等基础知识,考查学生的分析问题解决问题的能力、计算能力.在第二问易错
正确答案
(II)证明:由双曲线的性质可知,
由(I)可得,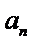
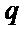
故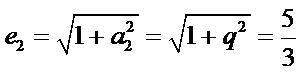
∴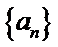
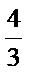
∴
∴
原式得证.
解析
(II)证明:由双曲线的性质可知,
由(I)可得,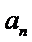
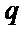
故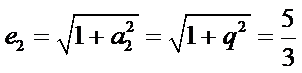
∴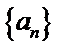
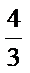
∴
∴
原式得证.
考查方向
解题思路
本题考查数列的通项公式、双曲线的离心率、等比数列的求和公式等基础知识,考查学生的分析问题解决问题的能力、计算能力.在第(Ⅱ)问中,不等式的证明用到了放缩法,这是证明不等式常用的方法,本题放缩的目的是为了求数列的和.另外放缩时要注意放缩的“度”.不能太大,否
易错点
本题考查数列的通项公式、双曲线的离心率、等比数列的求和公式等基础知识,考查学生的分析问题解决问题的能力、计算能力.在第二问易错
已知椭圆E: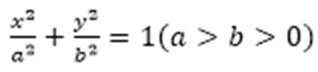
25.求椭圆E的方程及点T的坐标;
26.设O是坐标原点,直线l’平行于OT,与椭圆E交于不同的两点A、B,且与直线l交于点P.证明:存在常数λ,使得∣PT∣2=λ∣PA∣·∣PB∣,并求λ的值.
正确答案
(Ⅰ)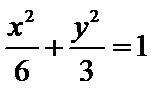
解析
(I)设短轴一端点为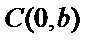
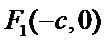
则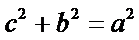
由题意,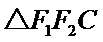
∴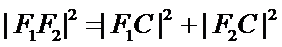
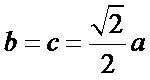
∴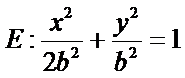
代入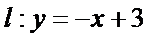
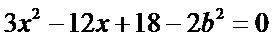
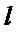
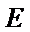
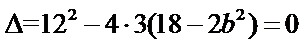
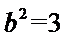
∴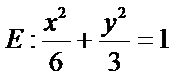
由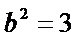
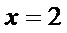
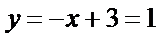
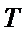
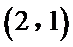
考查方向
解题思路
本题考查椭圆的标准方程及其几何性质,考查学生的分析问题解决问题的能力和数形结合的思想.在涉及到直线与椭圆(圆锥曲线)的交点问题时,一般都设交点坐标为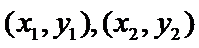
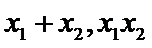
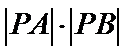
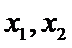

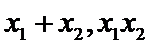
易错点
本题考查椭圆的标准方程及其几何性质,考查学生的分析问题解决问题的能力和数形结合的思想.易在第二问运算中出错。
正确答案
(Ⅱ)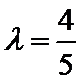
解析
(II)设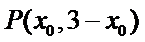
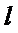
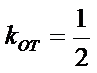
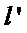
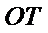
得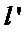
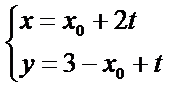
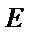
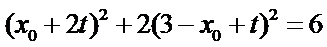
整理可得 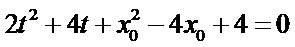
设两根为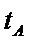
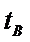
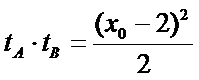
而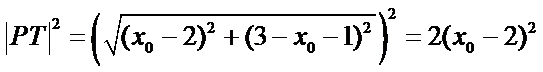
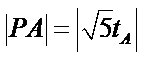
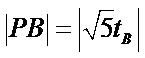
故有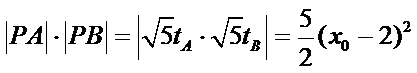
由题意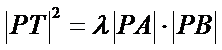
∴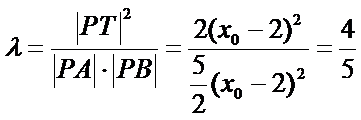
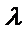
考查方向
解题思路
本题考查椭圆的标准方程及其几何性质,考查学生的分析问题解决问题的能力和数形结合的思想.在涉及到直线与椭圆(圆锥曲线)的交点问题时,一般都设交点坐标为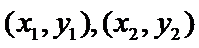
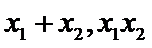
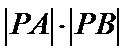
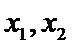

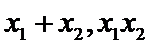
易错点
本题考查椭圆的标准方程及其几何性质,考查学生的分析问题解决问题的能力和数形结合的思想.易在第二问运算中出错。
在△ABC中,角A,B,C所对的边分别是a,b,c,且
19.证明:
20.若

正确答案
(Ⅰ)根据正弦定理,可设


则a=ksin A,b=ksin B,c=ksin C.
代入





sin Asin B=sin Acos B+cos Asin B=sin(A+B).
在△ABC中,由A+B+C=π,有sin(A+B)=sin(π–C)=sin C,
所以sin Asin B=sin C.
解析
(I)证明:由正弦定理
∵





考查方向
解题思路
本题考查正弦定理、余弦定理、商数关系等基础知识,考查学生的分析问题的能力和计算能力.在解三角形的应用中,凡是遇到等式中有边又有角时,可用正弦定理进行边角互化,一种是化为三角函数问题,一般是化为代数式变形问题.在角的变化过程中注意三角形的内角和为
易错点
本题考查正弦定理、余弦定理、商数关系等基础知识,在用化边为角的技巧应用中有时会发生错误。
正确答案
(Ⅱ)4.
解析
(II)由题
∵

则



考查方向
解题思路
本题考查正弦定理、余弦定理、商数关系等基础知识,考查学生的分析问题的能力和计算能力.在解三角形的应用中,凡是遇到等式中有边又有角时,可用正弦定理进行边角互化,一种是化为三角函数问题,一般是化为代数式变形问题.在角的变化过程中注意三角形的内角和为
易错点
本题考查正弦定理、余弦定理、商数关系等基础知识,在用化边为角的技巧应用中有时会发生错误。
我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准


16.求直方图中a的值;
17.设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
18.若该市政府希望使85%的居民每月的用水量不超过标准

正确答案
(Ⅰ)
解析
(I)由概率统计相关知识,各组频率之和的值为1
∵频率=(频率/组距)*组距
∴
得
考查方向
解题思路
本题主要考查频率分布直方图、频率、频数的计算公式等基础知识,考查学生的分析问题解决问题的能
易错点
本题主要在计算中易错
正确答案
(Ⅱ)36000;
解析
(II)由图,不低于3吨人数所占百分比为
∴全市月均用水量不低于3吨的人数为:
考查方向
解题思路
本题主要考查频率分布直方图、频率、频数的计算公式等基础知识,考查学生的分析问题解决问题的能
易错点
本题主要在计算中易错
正确答案
(Ⅲ)2.9
解析
(Ⅲ)因为前6组的频率之和为0.04+0.08+0.15+0.20+0.26+0.15=0.88>0.85,
而前5组的频率之和为0.04+0.08+0.15+0.20+0.26=0.73<0.85,
所以2.5≤x<3.
由0.3×(x–2.5)=0.85–0.73,
解得x=2.9.
所以,估计月用水量标准为2.9吨时,85%的居民每月的用水量不超过标准.
考查方向
解题思路
本题主要考查频率分布直方图、频率、频数的计算公式等基础知识,考查学生的分析问题解决问题的能
易错点
本题主要在计算中易错
设函数f(x)=ax2-a-lnx,其中a
27.讨论f(x)的单调性;
28.确定a的所有可能取值,使得f(x) >-e1-x+在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数).
正确答案
(Ⅰ)当





解析
(I)由题意,
①当




②当



当

故


考查方向
解题思路
本题考查导数的计算、利用导数求函数的单调性,最值、解决恒成立问题,考查学生的分析问题解决问题的能力和计算能力.求函数的单调性,基本方法是求







易错点
本题考查导数的计算、利用导数求函数的单调性,最值、解决恒成立问题,考查学生的分析问题解决问题的能力和计算能力,本题中注意由于函数
正确答案
(Ⅱ)
解析
(II)原不等式等价于

一方面,令
只需

又∵


令


另一方面,
当
∵




∴当


∴


∴


综上,
考查方向
解题思路
本题考查导数的计算、利用导数求函数的单调性,最值、解决恒成立问题,考查学生的分析问题解决问题的能力和计算能力.求函数的单调性,基本方法是求







易错点
本题考查导数的计算、利用导数求函数的单调性,最值、解决恒成立问题,考查学生的分析问题解决问题的能力和计算能力,本题中注意由于函数