- 真题试卷
- 模拟试卷
- 预测试卷
4. 如图,若一个空间几何体的三视图中,正视图和侧视图都是直角三角形,其直角边长均为1,则该几何体的表面积为 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 已知复数Z1

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 若函数






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若“


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.袋中标号为1,2,3,4的四只球,四人从中各取一只,其中甲不取1号球,乙不取2号球,丙不取3号球,丁不取4号球的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.关于



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知


正确答案


解析
解析已在路上飞奔,马上就到!
知识点
13.在极坐标系中,曲线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 将全体正整数自小到大一个接一个地顺次写成一排,如第11个数字是0,则从左至右的第
正确答案
7
解析
解析已在路上飞奔,马上就到!
知识点
15. 设二次函数
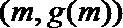
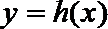
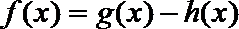
①存在相异的实数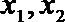
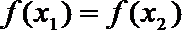
②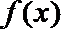
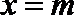
③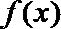
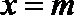
④不等式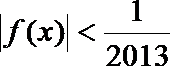
⑤直线 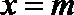
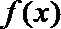
正确答案
① ④ ⑤
解析
解析已在路上飞奔,马上就到!
知识点
17. 淮南八公山某种豆腐食品是经过A、B、C三道工序加工而成的,A、B、C工序的产品合格率分别为


(Ⅰ)正式生产前先试生产2袋食品,求这2袋食品都为废品的概率;
(Ⅱ)设ξ为加工工序中产品合格的次数,求ξ的分布列和数学期望.
正确答案
(Ⅰ)2袋食品都为废品的情况为:
①2袋食品的三道工序都不合格;
②有一袋食品三道工序都不合格,另一袋有两道工不合格

③两袋都有两道工序不合格
所以2袋食品都为废品的概率为
(Ⅱ)由题意可得 ξ=0,1,2,3,



故 P(ξ=2)=1﹣P(ξ=0)﹣P(ξ=1)﹣P(ξ=3)=
得到ξ的分布列如下:
∴
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知函数






(1)试求
(2)求
(3)证明:当

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.在△ABC中,AB=c,AC=b,D为线段BC上的一点,且∠BAD=α,∠CAD=β,线段AD=l.
(1)求证:
(2)若AB=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 设函数

(1)若


(2)如果

(3)是否存在最小的正整数


正确答案
则

(3)对于函数

则



又


取

显然,存在最小的正整数


解析
解析已在路上飞奔,马上就到!
知识点
18. 某工厂某种产品的年固定成本为250万元,每生产



(1)写出年利润

(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
正确答案
(1)因为每件商品售价为0.05万元,则

依题意得:当


当


所以
(2)当
此时,当


当


即

所以,当产量为100千件时,该厂在这一商品中所获利润最大,最大利润为1000万元.
解析
解析已在路上飞奔,马上就到!
知识点
16.如图,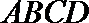
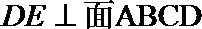
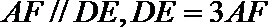
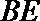
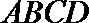
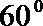
(1)求二面角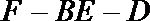
(2)设点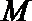
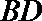
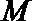
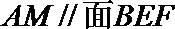
正确答案
解析
解析已在路上飞奔,马上就到!