- 真题试卷
- 模拟试卷
- 预测试卷
4.等差数列





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.一个棱锥的三视图如图,则该棱锥的全面积(单位:cm2)为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设随机变量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.在△ABC中,“

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 设F1、F2分别为椭圆


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 已知直线ax+by-1=0(a,b不全为0)与圆x2+y2=50有公共点,且公共点的横、纵坐标均为整数,那么这样的直线共有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知程序框图如下,则输出的
正确答案
9
解析
解析已在路上飞奔,马上就到!
知识点
14. 对一切实数x,不等式x2+a|x|+1≥0恒成立,则实数a的取值范围是___________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.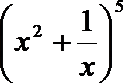
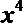
正确答案
10
解析
解析已在路上飞奔,马上就到!
知识点
13.已知实数



正确答案
-1
解析
解析已在路上飞奔,马上就到!
知识点
15. 在△OAB中,O为坐标原点,A(1,cosθ),B(sinθ,1) θ∈
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数



(1)求
(2)在







正确答案
解:(1)




由题意可知


即

(2)由(1)可知



而


由余弦定理知

.联立解得

解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数


(1)求数列

(2)若数列



正确答案
解:(1)
解析
解析已在路上飞奔,马上就到!
知识点
19.甲、乙两名同学在5次英语口语测试中的成绩统计如下面的茎叶图所示.
(1)现要从中选派一人参加英语口语竞赛,从统计学角度,你认为派哪位学生参加更合适,请说明理由;
(2)若将频率视为概率,对学生甲在今后的三次英语口语竞赛成绩进行预测,记这三次成绩中高于80分的次数为


正确答案
解:(1)
=

(2)高于80分的频率为






解析
解析已在路上飞奔,马上就到!
知识点
20.已知双曲线




(1)求双曲线
(2)










正确答案
解:(1)∵双曲线


由过



故双曲线
(2)设直线



圆心



由

则
又

由


∴直线

解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)求函数
(2)若


(3)在(2)的条件下,证明:
正确答案
解:(1)由题意
由

当



∴


即

其最小值为
(2)



由(1),设

由

易知


∴ 


因此


(3)由(2)知,对任意实数


令


∴ 
∴ 
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,四棱锥





(1)证明:平面

(2)若



正确答案
解:(1)证明: ∵
∴
又∵

又∵

又∵

∵


(2)如图,分别以





则




设平面
由

解析
解析已在路上飞奔,马上就到!






































































