- 真题试卷
- 模拟试卷
- 预测试卷
3.若




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.某工厂将甲、乙等五名新招聘员工分配到三个不同的车间,每个车间至少分配一名员工,若甲、乙两名员工必须分到同一个车间,则不同分法的种数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设全集



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.一个几何体的三视图如图所示,则该几何体的体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.实数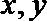
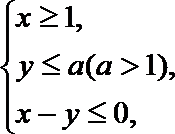
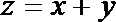
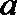
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.在整数集



①
②
③
④“整数


其中,正确结论的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.在等比数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知向量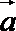
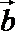
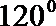
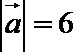
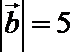
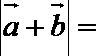
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 运行如下图所示的程序框图,则输出
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知双曲线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 已知函数


①点

②当

③关于

其中正确结论的题号为_________。
正确答案
①③
解析
解析已在路上飞奔,马上就到!
知识点
选做题 (14~15题,只能从中选做一题)
14.(坐标系与参数方程选做题)
在直角坐标系中,曲线







15.(几何证明选讲选做题)
如图, 








正确答案
14.
15.
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,一个圆形游戏转盘被分成6个均匀的扇形区域.用力旋转转盘,转盘停止转动时,箭头A所指区域的数字就是每次游戏所得的分数(箭头指向两个区域的边界时重新转动),且箭头A指向每个区域的可能性都是相等的.在一次家庭抽奖的活动中,要求每个家庭派一位儿童和一位成人先后分别转动一次游戏转盘,得分情况记为(a,b)(假设儿童和成人的得分互不影响,且每个家庭只能参加一次活动).
(Ⅰ)求某个家庭得分为(5,3)的概率;
(Ⅱ)若游戏规定:一个家庭的得分为参与游戏的两人得分之和,且得分大于等于8的家庭可以获得一份奖品.求某个家庭获奖的概率;
(Ⅲ)若共有4个家庭参加家庭抽奖活动.在(Ⅱ)的条件下,记获奖的家庭数为X,求X的分布列及数学期望.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,在矩形









(1)求证:
(2)求直线

(3)求点

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,已知抛物线










(1)求抛物线
(2)当


(3)若直线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.设










(1)设函数


①求证:函数

②求函数
(2)已知函数










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数
(1)求函数
(2)在








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知等差数列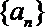
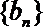
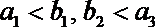
(1)求a的值;
(2)若对于任意的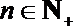
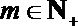
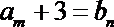
(3)令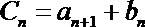
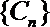
正确答案
解析
解析已在路上飞奔,马上就到!