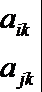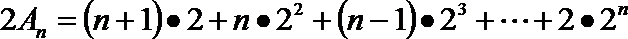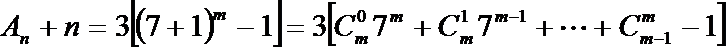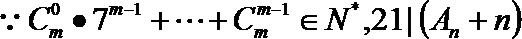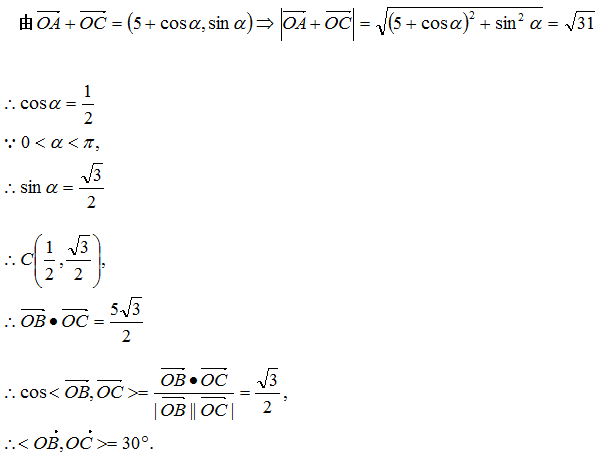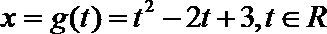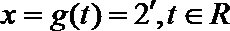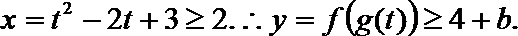- 真题试卷
- 模拟试卷
- 预测试卷
5.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.在







正确答案
(-6,21)
解析
解析已在路上飞奔,马上就到!
知识点
7.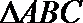
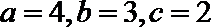
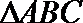
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.无穷数列
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.下图中的程序框图所描述的算法称为欧几里得辗转相除法,若输入

正确答案
67
解析
解析已在路上飞奔,马上就到!
知识点
10.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知数列
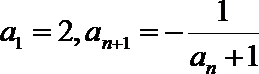
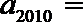
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.增广矩阵为


正确答案
(3,-1)
解析
解析已在路上飞奔,马上就到!
知识点
4.若对任意实数x ,有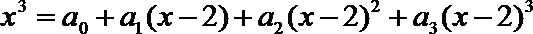
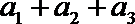
正确答案
19
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.若


正确答案
15
解析
解析已在路上飞奔,马上就到!
知识点
11.三个实数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.下列说法:
①若非零向量

②


③函数



④已知



⑤函数


其中正确的命题序号为_____________
正确答案
②③④
解析
解析已在路上飞奔,马上就到!
知识点
15.若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知a是实数,则函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.集合
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图所示的三角形数阵叫“莱布尼茨调和三角形”,它们是由整数的倒数组成的,第n行有n个数且两端的数均为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知命题


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.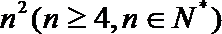
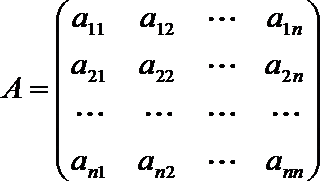
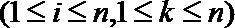
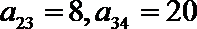
(1) 求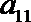
(2) 计算行数列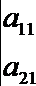
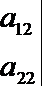
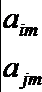
(3) 设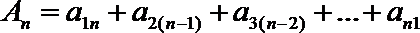
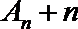
正确答案
解:(1)由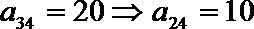
由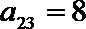
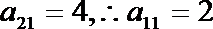
由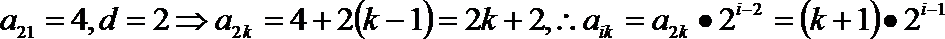
(2)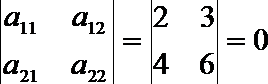
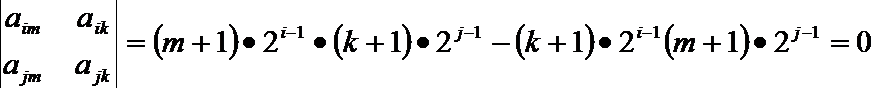
(3)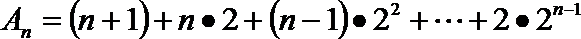
以上两式相减得: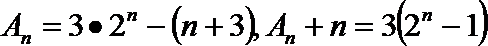
当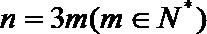
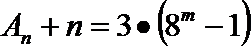
当m=1时,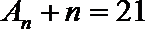
当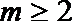
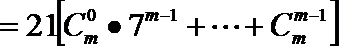
解析
解析已在路上飞奔,马上就到!
知识点
19.已知: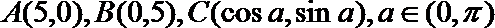
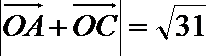
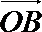
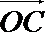
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.设函数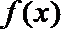
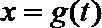
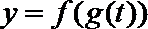
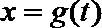
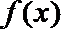
(1)判断下列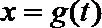
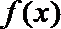
(A)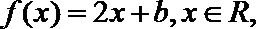
(B)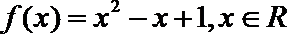
(2)设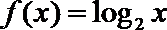
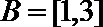
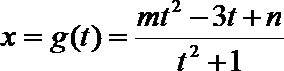
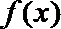
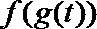
(3)设函数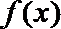
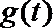
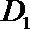
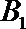
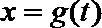
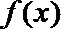
正确答案
(1)(A)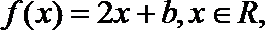
∴x=g(t)不是f(x)的一个等值域变换。
(B)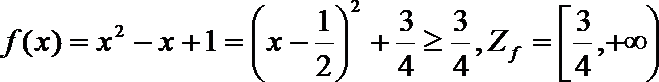
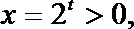
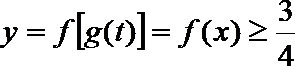
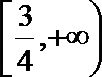
∴x=g(t)是f(x)的一个等值域变换。
(2)
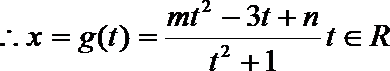
∴恒有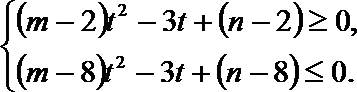
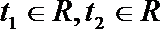
(3)设f(x)定义域为D值域为B。g(t)定义域为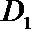
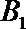
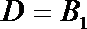
条件不必要性的一个例子:
的一个等值域变换
(反例不唯一)。
解析
解析已在路上飞奔,马上就到!
知识点
22.有两块扇形铁板,分别记为




(1)分别求出在


(2)试讨论

正确答案
(1)


∴当


(2)由
当
当
当
解析
解析已在路上飞奔,马上就到!