- 真题试卷
- 模拟试卷
- 预测试卷
1.集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知m、n是两条不重合的直线,
①若
②若
③若
④若m、n是异面直线,
其中真命题是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 为了得到函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.一个几何体的三视图如图所示,则该几何体的体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.对于定义在R上的函数
①若

②若函数


③若对

④函数

其中正确命题的个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.如下图所示的程序框图输出的结果是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.在一个袋子中装有分别标注数字1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同.现从中随机取出2个小球,则取出的小球标注的数字之和为3或6的概率是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.从双曲线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知平面内一点
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知直线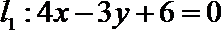
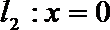
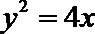
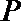
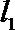
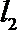
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
13.非零向量




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设实数


正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
11.

正确答案
11
解析
解析已在路上飞奔,马上就到!
知识点
15.已知三棱锥

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数



正确答案
(-1,1)
解析
解析已在路上飞奔,马上就到!
知识点
18.己知在锐角ΔABC中,角

(1)求角
(2)当

正确答案
(1)由已知及余弦定理,得

(2)由正弦定理,得
由
解析
解析已在路上飞奔,马上就到!
知识点
20.如图1,在平面内,














(1)求证:

(2)设二面角



正确答案
(1)连接











(2)
设
则
设平面
则
设平面
则



解得
解析
解析已在路上飞奔,马上就到!
知识点
19.
正确答案
(1)a



(2)S



当n为奇数时,,
3(1-ka










F(n)=


K
当n为偶数时,
3(1-ka






F(n)=

K
综合上面可得
解析
解析已在路上飞奔,马上就到!
知识点
22. 已知函数

(Ⅰ)若




(Ⅱ)若
(1)是否存在实数




(2)如果当


正确答案
(Ⅰ)∵



∴



∴
(Ⅱ)若


∴

(1)若





∴




当


(2)
△=







若




若

若








综上
解析
解析已在路上飞奔,马上就到!
知识点
21.已知A,B是椭圆


(1)求椭圆C的方程;
(2)求三角形MNT的面积的最大值
正确答案
(1)椭圆C的方程
(2)由点差法知PQ的中垂线交x轴于
设


令
故
解析
解析已在路上飞奔,马上就到!