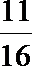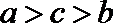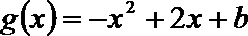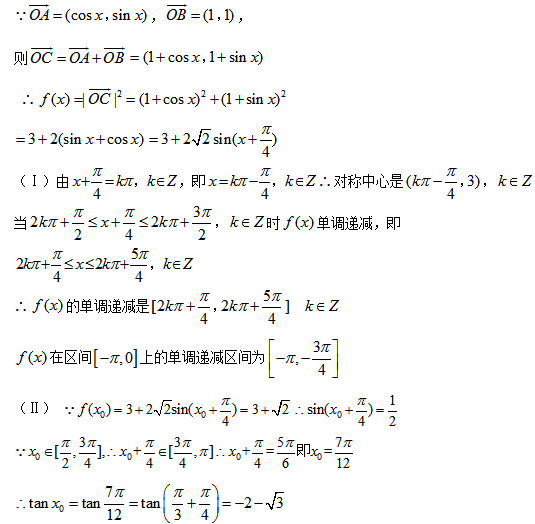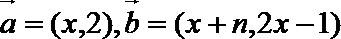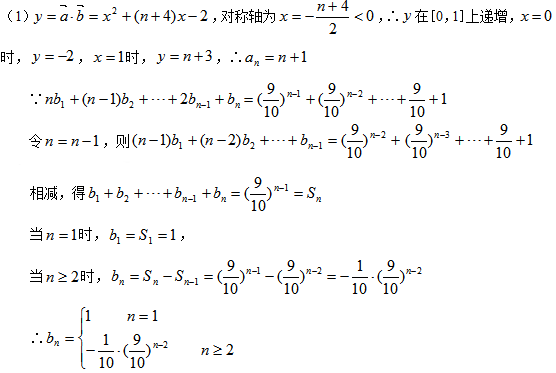- 真题试卷
- 模拟试卷
- 预测试卷
2.设复数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知向量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合



正确答案
0或3
解析
解析已在路上飞奔,马上就到!
知识点
3.已知





正确答案
若

解析
解析已在路上飞奔,马上就到!
知识点
4.在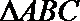
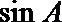
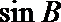
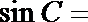
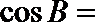
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知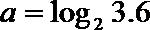
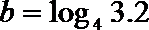
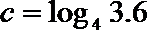
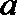
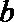
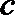
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.下列命题中,真命题是__________(写出所有真命题的序号)
①


②

③


④



正确答案
③④
解析
解析已在路上飞奔,马上就到!
知识点
8.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.回文数是指从左到右读与从右到右读都一样的正整数,如22,121,3443,94249等,显然2位回文数有9个:11,22,…99,3位回文数有90个:101,111,121,…191,202,…999,则5位回文数有________个。
正确答案
900
解析
解析已在路上飞奔,马上就到!
知识点
13.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知二次函数


正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
14.已知关于



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知集合

(Ⅰ)求集合

(Ⅱ)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数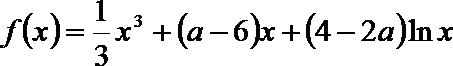
(Ⅰ)若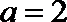
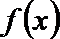
(Ⅱ)在(Ⅰ)的条件下,对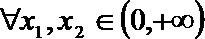
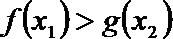
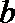
(Ⅲ)若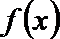
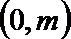
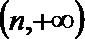
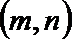
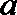
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.在直角坐标系中,已知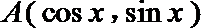
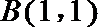
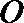
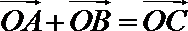
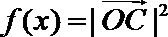
(Ⅰ)求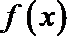
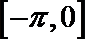
(Ⅱ)若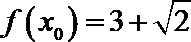
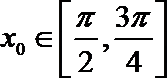
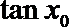
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数
(Ⅰ)求函数
(Ⅱ)设






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.设向量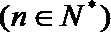
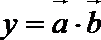
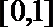
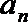
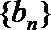
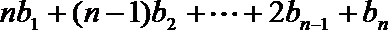
(1)求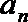
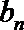
(2)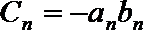
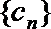
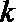
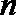
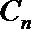
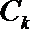
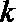
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数

(Ⅰ)求证:
(Ⅱ)当





正确答案
解析
解析已在路上飞奔,马上就到!