- 真题试卷
- 模拟试卷
- 预测试卷
1.已知全集



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.如图所示,程序框图输出的所有实数对
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.式子


①
②
③

其中,为轮换对称式的个数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.在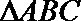
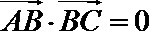
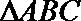
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张.从中任取3张,要求这3张卡片不能是同一种颜色,且红色卡片至多1张。不同取法的种数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.设





正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
16.如图,在正方形





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知某几何体的三视图如图,其中正视图中半圆的半径为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.
正确答案
40
解析
解析已在路上飞奔,马上就到!
知识点
17.若在曲线

①
②
③
④
对应的曲线中存在“自公切线”的有___________。
正确答案
23
解析
解析已在路上飞奔,马上就到!
知识点
14.函数







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.某单位实行休年假制度三年来,
根据上表信息解答以下问题:
(1)从该单位任选两名职工,用






(2)从该单位任选两名职工,用


正确答案
解:(1) 函数


则必有

所以,
当




所以
(2) 从该单位任选两名职工,用
则

于是


从而


解析
解析已在路上飞奔,马上就到!
知识点
20.在等腰梯形









(1)求证:

(2)求证:

(3)求二面角
正确答案
(1)证明:因为


所以
所以四边形
又因为等腰梯形,
所以 

所以
由已知可知 平面

因为 平面
所以
(2)证明:因为

所以平面
又因为


(3)因为



设




则
设平面



设平面

得
所以
由图形可知二面角
所以二面角

解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数
(Ⅰ)求
(Ⅱ)在





正确答案
(Ⅰ)

周期为
(Ⅱ)因为
所以
因为
所以
整理得
所以 三角形ABC为等边三角形
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数

(1)若


(2)若

(3)试比较


正确答案
(1)当



当




故




(2)
①若
当




当




②若
当








当





则在区间

综上: 当



当


(3)由(1)可知,当

则有


故:
解析
解析已在路上飞奔,马上就到!
知识点
21.已知抛物线的顶点在坐标原点,焦点在

(Ⅰ)求抛物线的标准方程;
(Ⅱ)与圆





正确答案
(Ⅰ)
(Ⅱ)由圆心

设交点
由
其中

得
即


解析
解析已在路上飞奔,马上就到!





























































































