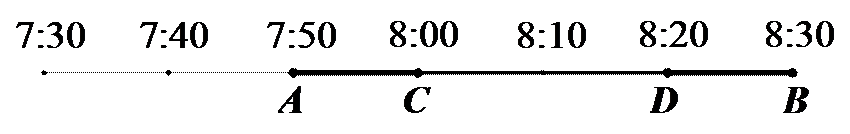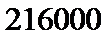- 真题试卷
- 模拟试卷
- 预测试卷
1.设集合

正确答案
解析
试题分析:因为

考查方向
解题思路
先分别求出两个集合中代表元素的取值范围,再求交集。
易错点
对一元二次不等式不熟悉导致出错。
知识点
3.已知等差数列

正确答案
解析
试题分析:由已知,

考查方向
解题思路
先求出等差数列的首项和公差,然后再代入等差数列的通项公式即可求解。
易错点
对等差数列的基本量运算不熟悉导致出错。
知识点
4.某公司的班车在7:00,8:00,8:30发车,小明在7:50至8:30之间到达发车站乘坐班车,且到达发车站的时刻是随机的,则他等车时间不超过10分钟的概率是
正确答案
解析
试题分析:如图所示,画出时间轴:
小明到达的时间会随机落在途中线段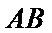
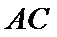
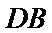
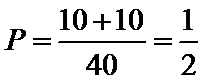
考查方向
解题思路
先确定几何度量,再根据几何概型的概率计算公式即可求解。
易错点
不能准确选择几何度量导致出错。
知识点
5.已知方程
正确答案
解析
试题分析:
∴


∴焦距


考查方向
解题思路
根据双曲线的定义及性质即可求解。
易错点
不注意双曲线的焦距是2c不是c,这一点易出错。
知识点
6.如图,某几


正确答案
解析
试题分析:该几何体直观图如图所示:
是一个球被切掉左上角的





考查方向
解题思路
由三视图可知该几何体的直观图如右图所示,则多面体的体积可求出。
易错点
不能将三视图还原为原图导致出错。
知识点
9.执行右面的程序框图,如果输入的
正确答案
解析
试题分析:当









考查方向
解题思路
求解此类问题一般是把人看作计算机,按照程序逐步列出运行结果。
易错点
不知何时终止循环导致出错。
知识点
2.设


正确答案
解析
因为

考查方向
解题思路
先求出x,y,再利用复数模的概念即可求出其模。
易错点
容易出现运算错误,特别是
知识点
7.函数

正确答案
解析
试题分析:函数











考查方向
解题思路
先根据函数奇偶性判断该函数为偶函数,进而确定图像关于y轴对称,再根据增减性即可确定答案。
易错点
不能综合应用函数的性质导致出错。
知识点
8.若
正确答案
解析
试题分析:用特殊值法,令






考查方向
解题思路
比较幂或对数值的大小,若幂的底数相同或对数的底数相同,通常利用指数函数或对数函数单调性进行比较,若底数不同,可考虑利用中间量进行比较.
易错点
不能灵活应用函数的性质导致出错。
知识点
10.以抛物线C的顶点为圆心的圆交C于A、B两点,交C的准线于D、E两点.已知|AB|=

正确答案
解析
试题解析:如图,设抛物线方程为














考查方向
解题思路
先设出抛物线的标准方程,再根据勾股定理求出P,进而求出焦点到准线的距离.
易错点
解题时一定要注意运算的准确性与技巧性,基础题失分过多是相当一部分学生数学考不好的主要原因。
知识点
11.平面



正确答案
解析
试题分析:如图,设平面
























考查方向
解题思路
求解本题的关键是作出异面直线所成角,求异面直线所成角的步骤是:平移定角、连线成形,解形求角、得钝求补.
易错点
相关定理不熟悉导致出错。
知识点
12.已知函数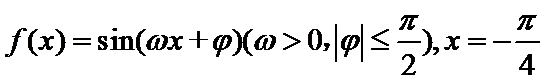
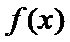
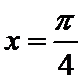
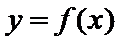
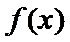
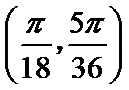
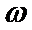
正确答案
解析
试题分析:因为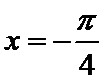
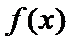
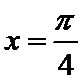
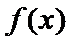
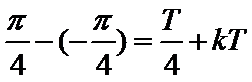
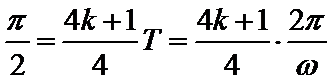
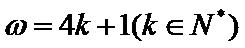
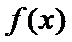
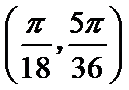
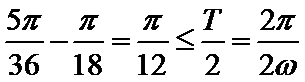
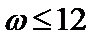
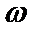
考查方向
解题思路
先根据函数的零点及对称性求出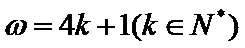
易错点
正弦函数的性质不熟悉导致出错。
知识点
13.设向量a=(m,1),b=(1,2),且|a+b|2=|a|2+|b|2,则m= .
正确答案
解析
试题分析:由



考查方向
解题思路
先根据|a+b|2=|a|2+|b|2 求出
易错点
相关知识点不熟悉导致出错。
知识点
14.
正确答案
解析
试题分析:





考查方向
解题思路
先写出通项
易错点
不能准确记忆二项式定理的通项公式导致出错。
知识点
15.设等比数列
正确答案
解析
试题分析:设等比数列的公比为








考查方向
解题思路
先根据等比数列的通项公式求出通项,进而即可求出a1a2 …an的最大值。
易错点
不能准确记忆等比数列的通项公式、性质导致出错。
知识点
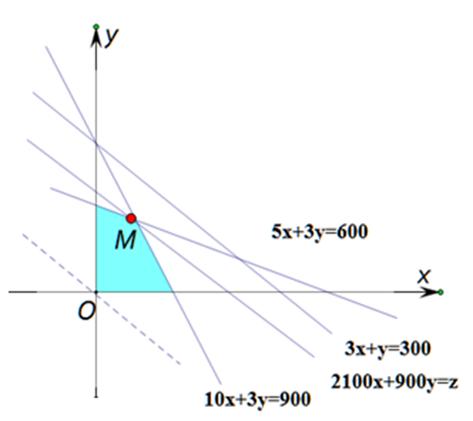
16.某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3kg,用3个工时.生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150kg,乙材料90kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为 元.
正确答案
解析
试题分析:设生产产品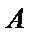
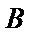
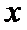
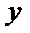
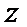
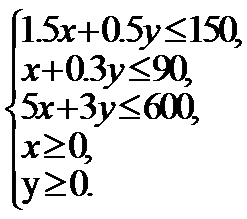
目标函数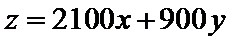
二元一次不等式组①等价于
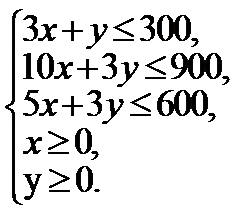
作出二元一次不等式组②表示的平面区域(如图),即可行域.
将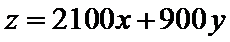
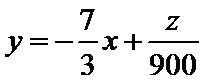
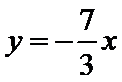
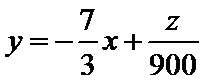
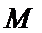
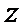
解方程组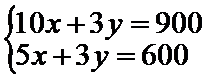
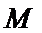
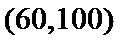
所以当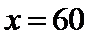
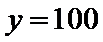
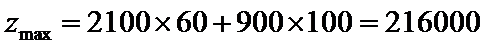
故生产产品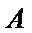
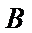
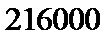
考查方向
解题思路
根据约束条件画出可行域,作出直线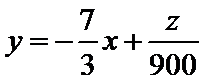
易错点
本题运算量较大,失分的一个主要原因是运算失误。
知识点

17.求C;
18.若


正确答案
解析
试题分析:本题属于正余弦定理的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
由正弦定理得:
∵
∴
∴
∵
∴
考查方向
解题思路
先利用正弦定理进行边角代换化简得得

易错点
相关知识点不熟容易处错。
正确答案
解析
试题分析:本题属于正余弦定理的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
由余弦定理得:
∴
∴
∴
考查方向
解题思路
根据






易错点
相关知识点不熟容易处错。
某公司计划购买2台机器,该种机器使用三年后即被淘汰.机器有一易损零件,在购进机器时,可以额外购买这种零件作为备件,每个200元.在机器使用期间,如果备件不足再购买,则每个500元.现需决策在购买机器时应同时购买几个易损零件,为此搜集并整理了100台这种机器在三年使用期内更换的易损零件数,得下面柱状图:
以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率,记

21.求
22.若要求

23.以购买易损零件所需费用的期望值为决策依据,在

正确答案
解析
试题分析:本题把随机变量的分布列与统计及函数结合在一起进行考查,有一定综合性但难度不是太大大,求解关键是读懂题意,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
每台机器更换的易损零件数为8,9,10,11
记事件

记事件

由题知
设2台机器共需更换的易损零件数的随机变量为

所以
考查方向
解题思路
试题分析:先确定X的取值分别为16,17,18,18,20,21,22,,再用相互独立事件概率模型求概率,然后写出分布列;
易错点
相关知识点不熟容易处错。
正确答案
19
解析
试题分析:本题把随机变量的分布列与统计及函数结合在一起进行考查,有一定综合性但难度不是太大大,求解关键是读懂题意,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
由(Ⅰ)知


考查方向
解题思路
试题分析:通过频率大小进行比较;
易错点
相关知识点不熟容易处错。
正确答案
解析
试题分析:本题把随机变量的分布列与统计及函数结合在一起进行考查,有一定综合性但难度不是太大大,求解关键是读懂题意,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
记
当

当

可知当


考查方向
解题思路
试题分析:分别求出n=9,n=20的期望,根据


易错点
相关知识点不熟容易处错。
设圆
24.证明
25.设点E的轨迹为曲线C1,直线l交C1于M,N两点,过B且与l垂直的直线与圆A交于P,Q两点,学.科网求四边形MPNQ面积的取值范围.
正确答案


解析
试题分析:本题属于圆锥曲线的综合应用问题,属于拔高题,不容易得分,解析如下:
因为


所以

又圆



由题设得





考查方向
解题思路
根据
易错点
对题中条件的处理容易出错。
正确答案
解析
试题分析:本题属于圆锥曲线的综合应用问题,属于拔高题,不容易得分,解析如下:
当





由

则

所以
过点









可得当



当





综上,四边形

考查方向
解题思路
分斜率是否错在射出直线方程,当直线斜率存在时设其方程为
易错点
对题中条件的处理容易出错。
如图,在以A,B,C,D,E,F为顶点的五面体中,面ABEF为正方形,AF=2FD, 

19.证明:平面ABEF
20.求二面角E-BC-A的余弦值.
正确答案
见解析
解析
试题分析:本题属于立体几何的综合应用问题,属于中档题,只要掌握相关立体几何的知识,即可解决本题,解析如下:
由已知可得



又



考查方向
解题思路
先证明

易错点
解题步骤不完整或考虑不全致推理片面导致出错。
正确答案
解析
试题分析:本题属于立体几何的综合应用问题,属于中档题,只要掌握相关立体几何的知识,即可解决本题,解析如下:
过




以




由(I)知








由已知,


又平面



由






所以



设



所以可取
设


同理可取

故二面角

考查方向
解题思路
建立空间直角坐标系,分别求出两个平面的法向量,再利用公式即可求出二面角.
易错点
解题步骤不完整或考虑不全致推理片面导致出错。
已知函数
26.求a的取值范围;
27.设x1,x2是

正确答案

解析
试题分析:本题属于导数的综合应用问题,属于拔高题,不容易得分,解析如下:
(Ⅰ)
(i)设


(ii)设







又





故
(iii)设



若








若













考查方向
解题思路
求导,根据导函数的符号来确定,主要要根据导函数的零点来分类讨论;
易错点
第二问对题中所给条件不知如何下手导致失分。
正确答案
见证明。
解析
试题分析:本题属于导数的综合应用问题,属于拔高题,不容易得分,解析如下:
由已知得:


故可整理得:
设
那么






设
设
则


因此,对于任意的

由




令
而



整理得:
考查方向
解题思路
借助第一问的结论来证明.
易错点
第二问对题中所给条件不知如何下手导致失分。
请考生在以下3题中任选一题作答,如果多做,则按所做的第一题计分,做答时请写清题号
【选修4-1:几何证明选讲】(请回答28、29题)
如图,△OAB是等腰三角形,∠AOB=120°.以O为圆心,
【选修4—4:坐标系与参数方程】(请回答30、31题)
在直角坐标系x

在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=
【选修4—5:不等式选讲】(请回答32、33题)
已知函数
28.证明:直线AB与
29.点C,D在⊙O上,且A,B,C,D四点共圆,证明:AB∥CD.
30.说明C1是哪一种曲线,并将C1的方程化为极坐标方程;
31.直线C3的极坐标方程为


32.在答题卡第(24)题图中画出
33.求不等式
正确答案
见解析
解析
试题分析:本题属于圆的综合应用问题,属于简单题,只要掌握相关圆的知识,即可解决本题,解析如下:
设


因为


在






考查方向
解题思路
先证明

易错点
对相关定理不熟悉导致本题失分。
正确答案
见解析
解析
试题分析:本题属于圆的综合应用问题,属于简单题,只要掌握相关圆的知识,即可解决本题,解析如下:
因为





由已知得




同理可证,

考查方向
解题思路
(2)利用四点共圆,作直线

易错点
对相关定理不熟悉导致本题失分。
正确答案
圆,
解析
试题分析:本题属于坐标系与参数方程的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:


∴
∴


∵
∴

考查方向
解题思路
直接利用互化公式即可求出极坐标方程;
易错点
不能熟记极坐标方程与参数方程的互化公式及应用导致本题出错。
正确答案
1
解析
试题分析:本题属于坐标系与参数方程的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:








①—②得:
∴
考查方向
解题思路
把直线的参数方程化为普通方程,即可求解.
易错点
不能熟记极坐标方程与参数方程的互化公式及应用导致本题出错。
正确答案
解析
试题分析:本题属于不等式的选讲内容,不等式证明选讲多以绝对值不等式为载体命制试题,主要涉及图像、解不等式、由不等式恒成立求参数范围等,解决此类问题通常转换为分段函数求解,注意不等式的解集一定要写出集合形式,属于简单题,只要掌握相关不等式的知识,即可解决本题,解析如下:
如图所示:
考查方向
解题思路
先将函数写成分段函数,然后作图;
易错点
忽略不等式的解集一定要写出集合形式导致丢分。
正确答案
解析
试题分析:本题属于不等式的选讲内容,不等式证明选讲多以绝对值不等式为载体命制试题,主要涉及图像、解不等式、由不等式恒成立求参数范围等,解决此类问题通常转换为分段函数求解,注意不等式的解集一定要写出集合形式,属于简单题,只要掌握相关不等式的知识,即可解决本题,解析如下:
当


当



当



综上,


考查方向
解题思路
用零点分区间法分类讨论,然后取并集.
易错点
忽略不等式的解集一定要写出集合形式导致丢分。