- 真题试卷
- 模拟试卷
- 预测试卷
2.以下命题正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.在长方体





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.如图,一个几何体三视图的正视图和侧视图为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知抛物线










正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.阅读如下程序,若输出的结果为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.将函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知等差数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.如下图是某位篮球运动员8场比赛得分的茎叶图,其中一个数据染上污渍用
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.随机变量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.数列




正确答案
49
解析
解析已在路上飞奔,马上就到!
知识点
16.关于函数

①函数

②


③若函数
④


⑤函数
其中不正确的命题序号是________
正确答案
①②③⑤
解析
解析已在路上飞奔,马上就到!
知识点
14.由不等式组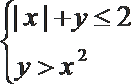
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.某旅游景点有一处山峰,游客需从景







(1)求B,D两点的海拔落差
(2)求AD的长.
正确答案
解:(1)
(2)法一:在

在

所以
法二:在

所以
解析
解析已在路上飞奔,马上就到!
知识点
19.“跑跑龟”是一款益智游戏,它灵活多变老少皆宜,深受大家喜爱。有位小朋友模仿“跑跑龟”也自己动手设计了一个简易游戏来自娱自乐,并且制定规则如下:如图为游戏棋盘由起点到终

(1)求恰好抽取4张卡片即结束游戏的概率;
(2)若游戏结束抽取的卡片张数记为

正确答案
(1)设抽取4张卡片即结束游戏为事件A,取4张步数要大于等于7,
卡片可以是2个A、1个2、1个3或1个A、2个2、1个3,
所以
(2)由题意





解析
解析已在路上飞奔,马上就到!
知识点
21.已知

(1)若直线


(2)是否存在实数



正确答案
解(1)设




设




(2)令

令




不妨令



所以
因为

所以
令

所以



又




解析
解析已在路上飞奔,马上就到!
知识点
18.如图,在四棱锥






(1)点



(2)若






正确答案
解法一:(1)因为


因为平面






所以




(2)如图,因为



所以





设面






所以



由平面



解法二:(1)同一
(2)在平面






设平面




由



解得



因为面




所以




解析
解析已在路上飞奔,马上就到!
知识点
20.在平面直角坐标系









(1)求曲线


(2)当








①证明:四边形
②若

正确答案
解:(1)设


①当


②当


③当


④当


(2)①当




设

所以四边形
②设



解析
解析已在路上飞奔,马上就到!
知识点
请从22~24三题中任选一题作答。
22.选修4—1:几何证明选讲
如图,⊙














证明:(1)
(2)
正确答案
22.
证明:(1)因为


又



由①②得
(2)连接






所以




23.解:(1)


24.解:(Ⅰ)

(Ⅱ)
函数


解析
解析已在路上飞奔,马上就到!









































































