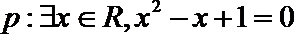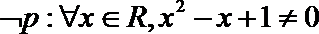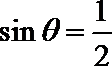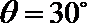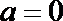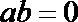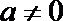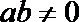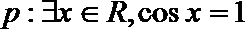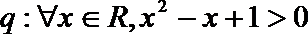理科数学 2014年高三试卷

精品

单选题
填空题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共10小题，每小题5分，共50分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

1.已知，则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

7. 过点（0，1）引x2+y2－4x+3=0的两条切线，这两条切线夹角的余弦值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线与平面平行的判定与性质

题型：单选题

分值: 5分

8. 函数的最小正周期为，为了得到函数的图象，只要将的图象（）

A向左平移个单位长度

B向右平移个单位长度

C向左平移个单位长度

D向右平移个单位长度

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

5. 函数的图象大致是（　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：单选题

分值: 5分

2.下列函数中，在其定义域内，既是奇函数又是减函数的是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：单选题

分值: 5分

3．下列说法错误的是（）

A若命题，则

B“”是“”的充分不必要条件

C命题“若，则”的否命题是：“若，则”

D已知，，则“”为假命题

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平行公理

题型：单选题

分值: 5分

4. 设，则的大小关系是（　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

对数函数的定义

题型：单选题

分值: 5分

9. 已知定义在R上的函数f（x）满足f（x＋1）＝－f（x）。当x［0,1］时，f（x）＝－x，若g（x）＝f（x）－m（x＋1）在区间（－1,2］有3个零点，则实数m的取值范围是（）

A（－，）

B（－，］

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：单选题

分值: 5分

6. 在极坐标系中，点到圆的圆心的距离为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

弧度制的应用

题型：单选题

分值: 5分

10. 已知函数，，，则的最小值等于（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

填空题本大题共5小题，每小题5分，共25分。把答案填写在题中横线上。

题型：填空题

分值: 5分

11.已知函数，若，则实数a等于_______

正确答案

0或2

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 5分

14. 在平面直角坐标系中，过椭圆的右焦点，且与直线（为参数）平行的直线截椭圆所得弦长为______

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

对数函数的定义域

题型：填空题

分值: 5分

13．某出租车公司规定乘车收费标准如下：3 km以内为起步价8元(即行程不超过3 km，一律收费8元)；若超过3 km，除起步价外，超过的部分再按1.5元/km计价；若司机再与某乘客约定按四舍五入以元计费不找零钱．已知该乘客下车时乘车里程数为7.4 km，则该乘客应付的车费为________

正确答案

15元

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 5分

12.曲线和曲线围成的图形面积是______

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：填空题

分值: 5分

15.下列命题：

①函数的单调区间是 .

②函数有2个零点.

③已知函数的图像为曲线C，若曲线C存在与直线垂直的切线，则实数m的取值范围是.

④若函数对任意的都有则实数的取值范围是（-].

其中正确命题的序号为_________

正确答案

②③

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

简答题（综合题）本大题共75分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

16.已知全集U=R，非空集合＜，＜.

（1）当时，求；

（2）命题，命题，若q是p的必要条件，求实数的取值范围。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

定积分

题型：简答题

分值: 12分

17．设函数，

（1）求的周期和对称中心；

（2）求在上值域。

正确答案

解：（1），

的周期

由得

所以的对称中心为

（2）因为，所以，

所以

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：简答题

分值: 13分

20. 已知函数

（1）若实数求函数在上的极值；

（2）记函数，设函数的图像与轴交于点，曲线在点处的切线与两坐标轴所围成图形的面积为则当时，求的最小值。

正确答案

解：（1）

当时，由

若，则，所以恒成立，

所以单调递增，无极值。

若，则单调递减；

单调递增。

所以有极小值。

（2）=

令得，即

点处切线斜率：

点处切线方程：

令得，令得

所以

令

当且仅当

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的图像

题型：简答题

分值: 12分

19. 如图：四棱锥P—ABCD中，底面ABCD是矩形，PA⊥底面ABCD，PA=AB=1，AD=，点F是PB的中点，点E在边BC上移动.

（1）证明：无论点E在BC边的何处，都有PE⊥AF;

（2）当BE等于何值时，PA与平面PDE所成角的大小为45°。

正确答案

解：（1）

则P（0，0，1），B（0，1，0），

设

∴AF⊥PE

（2）

解析

解析已在路上飞奔，马上就到！

知识点

平行公理

题型：简答题

分值: 14分

21.已知函数，若

（1）求曲线在点处的切线方程；

（2）若函数在区间上有两个零点，求实数b的取值范围；

（3）当。

正确答案

解:（1）因为，

所以曲线在点处的切线方程为

（2）=，(x>0)

=，由>0得x>1, 由<0得0<x<1.

所以的单调递增区间是（1，+）,单调递减区间（0, 1）

x=1时，取得极小值.

（3）当

即证：

构造函数：

当时，

所以，

又，所以

即

所以

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：简答题

分值: 12分

18. 已知函数（）在区间上有最大值和最小值．设，

（1）求、的值；

（2）若不等式在上有解，求实数的取值范围。

正确答案

解：（1），

因为，对称轴为，所以在区间上是先减后增，

故，解得．

（2）由（1）可得，

所以在上有解，

可化为在上有解。

即

令，因，故，

记，对称轴为：，

因为，单调递增，

故当时，最大值为

所以的取值范围是．

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的图象和性质二次函数在闭区间上的最值

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷