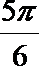- 真题试卷
- 模拟试卷
- 预测试卷
5.已知p: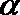
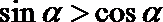
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设集合
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知t>0,若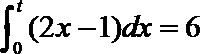
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.直线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.为得到函数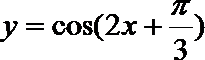
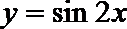
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.以下有关命题的说法错误的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若实数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.下列命题正确的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.方程

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知定义在R上的函数



正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数

①图象C关于直线
②图象C关于点
③由

④函数f(x)在区间(
⑤函数

其中正确的结论序号是____________.(把你认为正确的结论序号都填上)
正确答案
①②④
解析
解析已在路上飞奔,马上就到!
知识点
14.已知几何体的三视图如图所示,可得这个几何体的体积是 ___________
正确答案
6
解析
解析已在路上飞奔,马上就到!
知识点
13.设





正确答案
60°
解析
解析已在路上飞奔,马上就到!
知识点
19.在如图所示的几何体中,平面






(1)求证:

(2)求二面角
正确答案
(1)∵平面





又
且


(2)(解法一)建立如图空间直角坐标系
不妨设
则由题意得


设平面



设平面



所以
∴二面角

(解法二)取


因为

∴






则


由题意,不妨设
连接

因此在



因此二面角
解析
解析已在路上飞奔,马上就到!
知识点
20.已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元。设该公司一年内生产该品牌服装x千件并全部销售完,每千件的销售收入为
(1)写出年利润W(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得的年利润最大。
(注:年利润=年销售收入-年总成本)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知数列{

(I)求
(II)设


(III)设


正确答案
由条件可知
设
当

当
当




∴

解析
解析已在路上飞奔,马上就到!
知识点
17.若二次函数


(1) 求函数
(2)对任意的


正确答案
(1) ∵
∴
(2)由题意知:

整理得

令
∵
当


所以


注意也可用导数求解
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数

(1)曲线




(2)




(3)




正确答案
解:(1)

∵曲线


∴ 

(2)设

又在点
∴
设

∴



从而,结合(Ⅰ)可知,满足题设的点
(3)当



曲线



由

∵ 曲线



即

若




从而,方程

令

∴ 当






∴





解析
解析已在路上飞奔,马上就到!
知识点
18 .已知函数
(1)求函数
(2)已知






正确答案
(1)原式整理得
对称中心为
单调减区间为
(2)∵

∴C=
∵

及由正弦定理得
由余弦定理得
∴
解析
解析已在路上飞奔,马上就到!