- 真题试卷
- 模拟试卷
- 预测试卷
3.已知命题:“

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.在


正确答案

解析
解析已在路上飞奔,马上就到!
知识点
7.设实数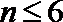
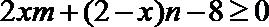
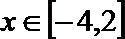
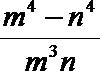
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.如图,在矩形







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知



正确答案
无
解析
解析已在路上飞奔,马上就到!
知识点
11.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合A=


正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
2.已知复数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知向量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.各项均为正数的等比数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
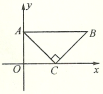
14.如图放置的等腰直角三角形ABC薄片(∠ACB=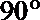
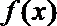
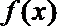
正确答案
2+4
解析
解析已在路上飞奔,马上就到!
知识点
12.已知数列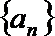
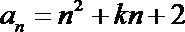
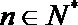
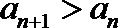
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.设函数









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.






正确答案

解析
解析已在路上飞奔,马上就到!
知识点
16.在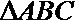



(1)求证: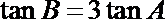
(2)若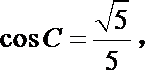
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知数列{an}的前n项和为Sn,a1=1,且
(1)求a2,a
(2)解不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(1)若a=1,f(x)在(0,+∞)上是单调增函数,求b的取值范围;
(2)若a≥2,b=1,求方程
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知a=(sinx,-cosx),b=(cosx,

(1)求f(x)的最小正周期,并求其图像对称中心的坐标;
(2)当0≤x≤
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.某校为扩大教学规模,从今年起扩大招生,现有学生人数为b人,以后学生人数年增长率为4.9‰.该校今年年初有旧实验设备a套,其中需要换掉的旧设备占了一半。学校决定每年以当年年初设备数量的10%的增长率增加新设备,同时每年换掉x套的旧设备。
(1)如果10年后该校学生的人均占有设备的比率正好比目前翻一番,那么每年应更换的旧设备是多少套?
(2)依照(1)的更换速度,共需多少年能更换所有需要更换的旧设备?
下列数据供计算时参考:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数f(x)=3-2log2x,g(x)=log2x。
(1) 求函数M(x)=
(2) 如果对f(x2)f(
正确答案
解析
解析已在路上飞奔,马上就到!