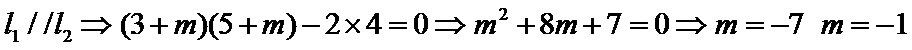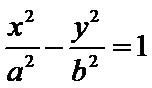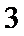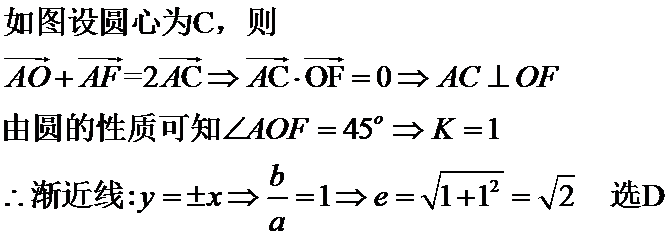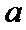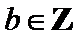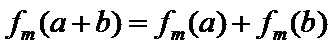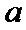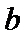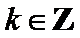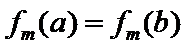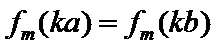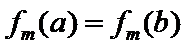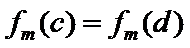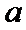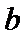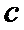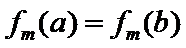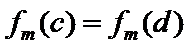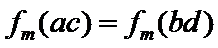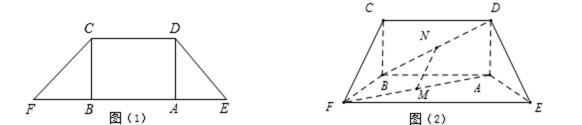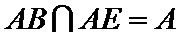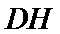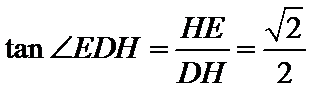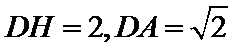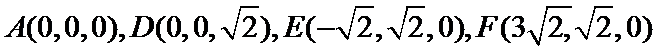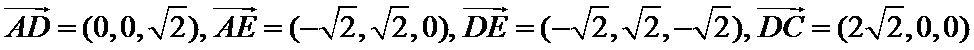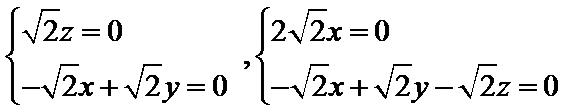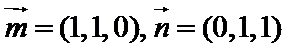- 真题试卷
- 模拟试卷
- 预测试卷
2.已知直线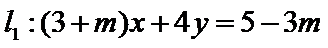
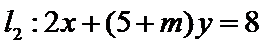
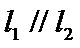
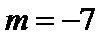
正确答案
解析
考查方向
解题思路
本题属于简单题,可使用直接法,
易错点
该题容易把两直线重合忽略
知识点
4.将函数



位,得到的函数的图像的一个对称中心为()
正确答案
解析


考查方向
易错点
本题易错在平移变化出错
解题思路】该题是常规题1、平移得到新函数
知识点
5.等差数列








正确答案
解析
考查方向
解题思路
1、使用一元二次不等式解集求参数的值d,a1,
2、使用通项公式确定前n项和的最大值
易错点
主要易错于最值的判断
知识点
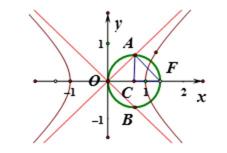
6.已知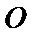

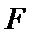
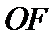
圆交双曲线的渐近线于两点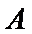
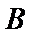
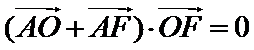
心率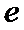
正确答案
解析
由题意作图
考查方向
解题思路
1、根据题意画出简图
2、找到向量的性质直接得出a,b的关系
易错点
主要易错于圆的性质的判断,以及向量的几何意义的判断
知识点
3.已知空间两条不同的直线


正确答案
解析
对于A:正确
对于B:正确应该是
对于C:
对于D:
考查方向
解题思路
本题属于常规题,可使用排除法解答,
易错点
该题易错于对判定定理不熟导致判断失误
知识点
7.设

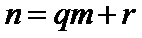
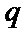
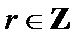
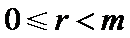
则记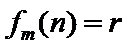
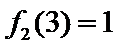
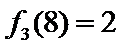
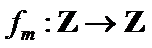
确的是()
正确答案
解析
考查方向
解题思路
该题的本质问题即n被m整除余r,对于ABCD,使用特例法,以及排除法得出答案
易错点
主要易错于对题意理解错误,导致无法解答
知识点
8.如图,在等腰梯形










使得

正确答案
解析
以DC所在直线为x轴,DC的中垂线为y轴建立平面直角坐标系,则梯形的高为
\
考查方向
解题思路
该题使用建立坐标系,设P的坐标,根据
易错点
主要易错于讨论不全,漏解
知识点
1.已知集合


正确答案
解析

考查方向
解题思路
本题属于简单题,可使用直接法,
(1)分别求解不等式,
(2)确定交集运算
易错点
计算过程对一元二次不等式出错,对对数函数的单调性判断错误,不能区分交并概念
知识点
10.已知

正确答案

解析
化简的
则
解不等式
∴单调递减区间为
考查方向
解题思路
1、由三角函数公式化简可得

易错点
主要易错于三角函数恒等变换出错
知识点
11.设函数






正确答案


解析
做函数
考查方向
解题思路
1、根据题意做出函数草图
2、结合图像给出范围
易错点
主要易错于对基本函数图像和复合函数理解错误
知识点
9.某几何体的三视图如图所示, 则该几何体的体积为______,表面积为______.
正确答案

解析
由三视图可知几何体为圆锥的 ,底面半径为1,高为2.母线为
∴几何体的体积
几何体的表面积
故答案为 
考查方向
解题思路
还原直观图可知是圆锥的一半,所以体积为圆锥的一半,求面积要注意截面
易错点
主要易错于三视图数据读取错误,忽视截面的面积
知识点
13.在



若

正确答案
解析
因为E在BD上
∴
考查方向
解题思路
1、建立基底,所有的向量使用基底表示,2、使用共线条件得出关系
易错点
主要易错于三点共线的转换
知识点
14.如图,在边长为


现将△



影






则点
正确答案
解析
由题意,在平面AED内过点D作
则
当E从点D运动到C,再从C运动到B,故H点的轨迹是以AD'为直径的半圆弧,
根据边长为2的正方形ABCD知圆半径是1,
所以其所对的弧长为π,
故答案为:π
考查方向
解题思路
根据图形的翻折过程中变与不变的量和位置关系知,在平面AED内过点D作

易错点
主要易错于信息的转化失败,导致计算出错
知识点
15.设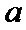
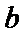
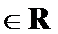
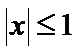
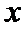
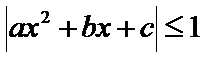
的最大可能值为______.
正确答案
3
解析
任意满足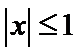
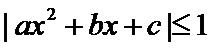
即有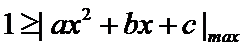
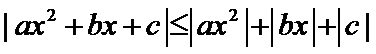
由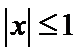
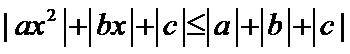
可得当且仅当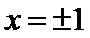
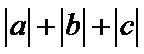
即有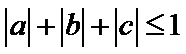
即有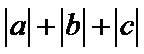
故答案为:1.
考查方向
解题思路
由题意可得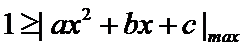
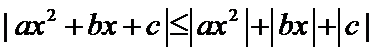
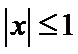
易错点
主要易错于不等式的转化,
知识点
12.动直线






正确答案

解析
整理直线方程得
做出不等式组的可行域得
①当直线K不存在时成立 即
②当 
由图可知与可行域有交点时,直线AP逆时针旋转,kAP变大
考查方向
解题思路
1、利用分离参数法,解方程组得出定点,2、画出可行域,题意转换为,直线绕定点旋转,即斜率问题
易错点
主要易错于对含参直线方程的理解出错
知识点
如图(1),在等腰梯形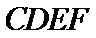
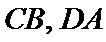

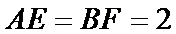
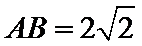
现将梯形沿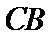
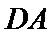
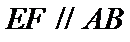
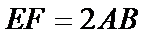
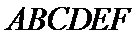
图(2)示,已知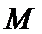
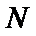
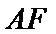
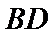
18.求证: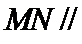
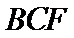
19.若直线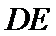
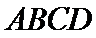
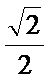
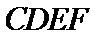
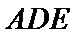
正确答案
见解析
解析
(Ⅰ)证明:连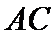
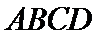
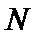
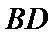
∴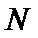
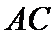
在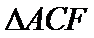
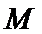
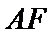
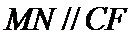
∵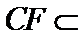
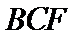
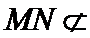
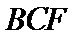
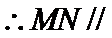
考查方向
解题思路
连结AC,通过证明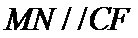
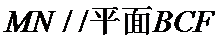
易错点
主要易错于线面角的判断出错,
正确答案
见解析
解析
(Ⅱ)依题意知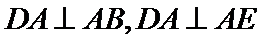
∴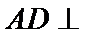
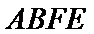
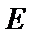
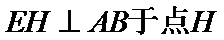
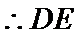
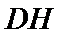
所以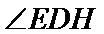
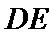
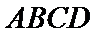
所以:
所以:
设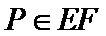
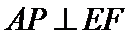
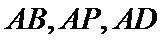

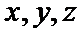
则
设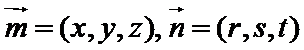
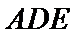
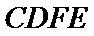
令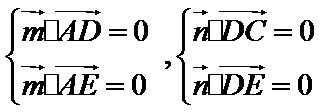
即
取
则
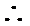
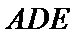
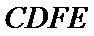
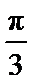
考查方向
解题思路
先由线面垂直的判定定理可证得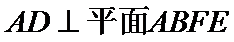
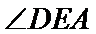
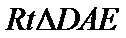
分别以AB,AP,AD所在的直线建立空间直角坐标系,求出平面ADE与平面CDFE的法向量,代入向量夹角公式,可得答案.
易错点
主要易错于线面角的判断出错,
已知数列

24.若

25.若



正确答案
见解析
解析
(1)
当
当
考查方向
解题思路
由数列

易错点
主要易错于递推关系找不出,
正确答案
见解析
解析
(2)方法1:

①/②得,因为
方法2:因为
又因为
所以

所以

所以:
考查方向
解题思路
这里可以从两个方面进行分析
①直接找出
②根据递推关系得出
易错点
主要易错于递推关系找不出,
如图所示,在四边形





16.求△
17.若

正确答案
见解析
解析
(Ⅰ)
因为

所以△ACD的面积
考查方向
解题思路
利用已知条件求出∠D角的正弦函数值,然后求
易错点
主要易错于计算出错,
正确答案
见解析
解析
(Ⅱ)在△ACD中,
所以
在△ABC中,
把已知条件代入并化简得:

考查方向
解题思路
利用余弦定理求出AC,通过
易错点
主要易错于计算出错,
20.求
21.当




22.求椭圆C1的方程;
23.求△EPM面积最大时直线l的方程.
正确答案
见解析
解析
(1)因为

又因为
解得:

即:
考查方向
解题思路
根据条件建立方程和基本不等式关系即可求
易错点
主要易错于去绝对值讨论出错,
正确答案
见解析
解析
(2)因为


则问题为 


即

令


由

整理得
问题转化为:求

① 当





② 当
又
综上,实数
考查方向
解题思路
求出
易错点
主要易错于去绝对值讨论出错,
正确答案
见解析
解析
(1)由题意得:

考查方向
解题思路
由圆的面积公式可得b=1,再由圆的性质
易错点
主要易错于点P,M及斜率的求解,
正确答案
见解析
解析
(2)由题意得:直线

不妨设直线

由:

所以:
由

所以:
设
当且仅当
则直线
所以所求直线
考查方向
解题思路
由题意得:直线PE,ME的斜率存在且不为0,


易错点
主要易错于点P,M及斜率的求解,