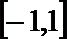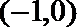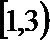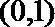- 真题试卷
- 模拟试卷
- 预测试卷
2.设集合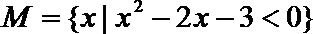
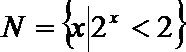
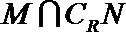
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.设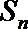
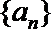
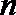
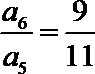
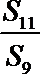
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知抛物线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 过抛物线





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.在复平面内,复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.“


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.关于函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.某程序框图如图所示,则该程序运行后输出
正确答案
7
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知实数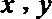
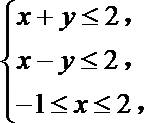
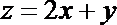
正确答案
-5
解析
解析已在路上飞奔,马上就到!
知识点
13.已知


正确答案
18
解析
解析已在路上飞奔,马上就到!
知识点
15.已知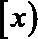

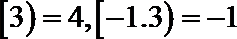
下列命题:
①函数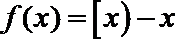
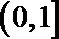
②若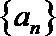
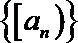
③若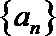
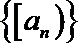
④若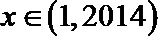
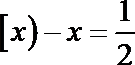
其中正确的的序号是____________.(把你认为正确的序号都填上)
正确答案
①④
解析
解析已在路上飞奔,马上就到!
知识点
14.将


正确答案
480
解析
解析已在路上飞奔,马上就到!
知识点
16.在△ABC中,角A,B,C的对边分别为a,b,c.设向量

(1)若

(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.在数列
(I)证明

(II)求

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.为了倡导健康、低碳、绿色的生活理念,某市建立了公共自行车服务系统鼓励
市民租用公共自行车出行,公共自行车按每车每次的租用时间进行收费,具体收费标准如下:
①租用时间不超过1小时,免费;
②租用时间为1小时以上且不超过2小时,收费1元;
③租用时间为2小时以上且不超过3小时,收费2元;
④租用时间超过3小时的时段,按每小时2元收费(不足1小时的部分按1小时计算)
已知甲、乙两人独立出行,各租用公共自行车一次,两人租车时间都不会超过3小时,设甲、乙租用时间不超过1小时的概率分别是0. 4和0. 5 ;租用时间为1小时以上且不超过2小时的概率分别是0.5和0.3.
(I)求甲、乙两人所付租车费相同的概率;
(II)设甲、乙两人所付租车费之和为随机变量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图,平面








(1)求证:

(2)求直线

(3)能否在


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆C:
(1)求椭圆C的方程;
(2)过点Q(4,0)且不与坐标轴垂直的直线l交椭圆C于A、B两点,设点A关于x轴的对称点为A1.求证:直线A1B过x轴上一定点,并求出此定点坐标.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数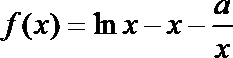
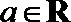
(1)当
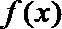
(2)求函数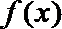
(3)当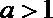
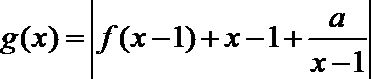
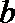
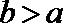
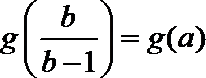
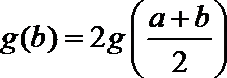
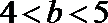
正确答案
解析
解析已在路上飞奔,马上就到!