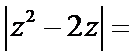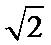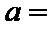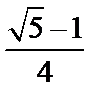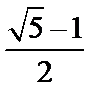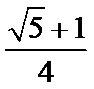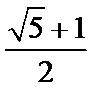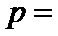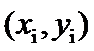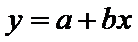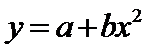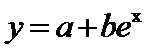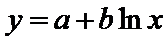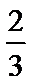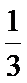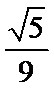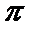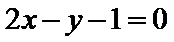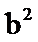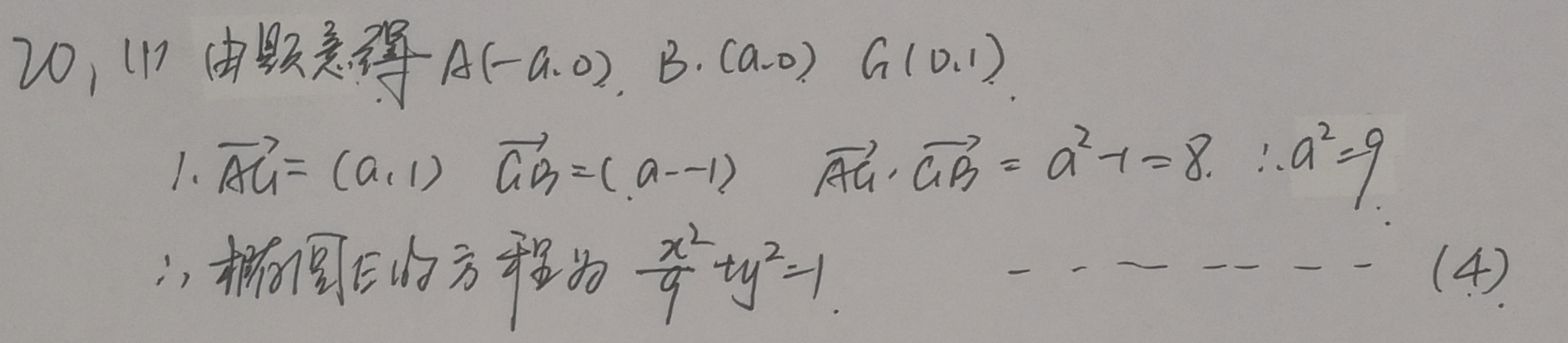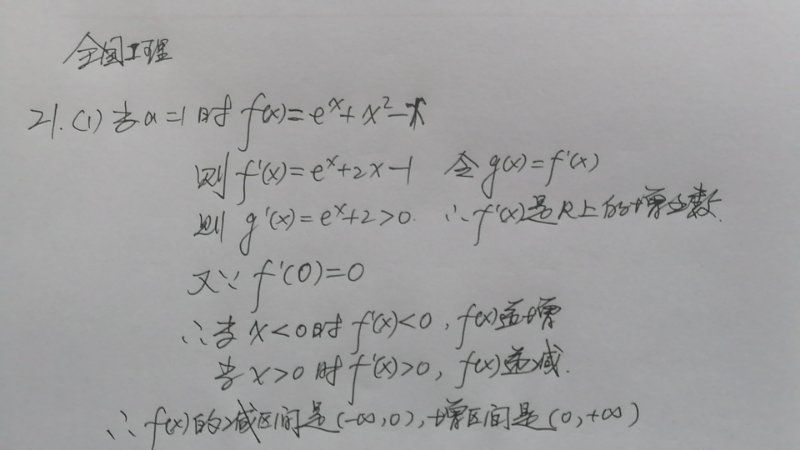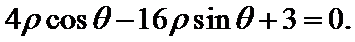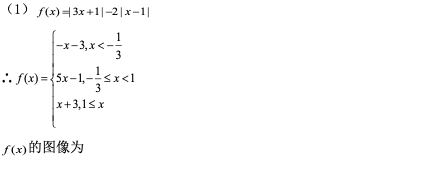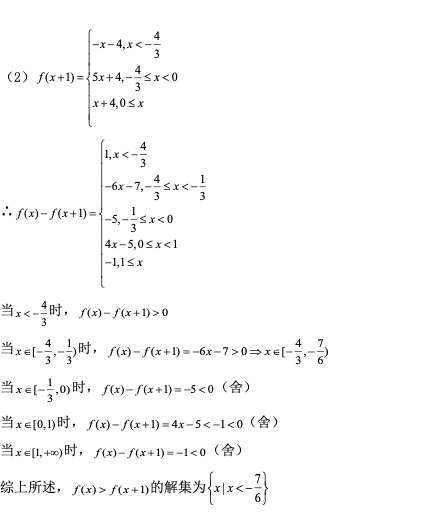- 真题试卷
- 模拟试卷
- 预测试卷
1. 若
正确答案
2.设集合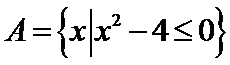
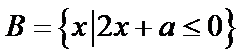
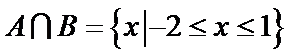
正确答案
3. 埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为
正确答案
6.函数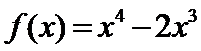
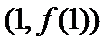
正确答案
7.设函数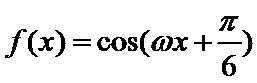
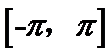
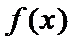
正确答案
4.已知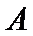
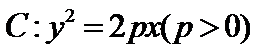
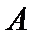
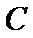
正确答案
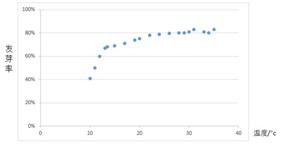
5.某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位: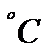
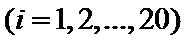
由此散点图,在10℃至40℃之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是
正确答案
9. 已知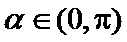
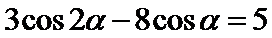
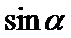
正确答案
8. 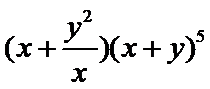
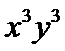
正确答案
10. 已知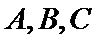

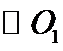
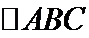
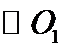
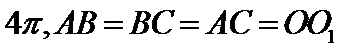

正确答案
11. 已知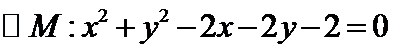
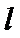
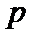
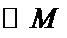
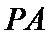
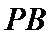
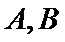
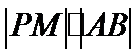
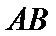
正确答案
12.若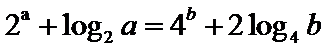
正确答案
13.若x,y满足约束条件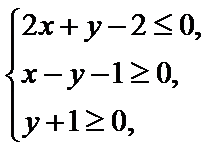
正确答案
1
14.设a,b为单位向量,且
正确答案
√3
15.已知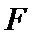
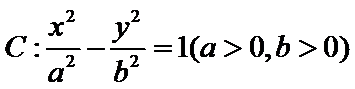
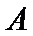
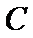
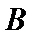
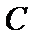
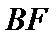
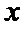
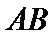
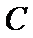
正确答案
2
16.如图,在三棱锥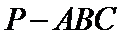
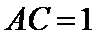
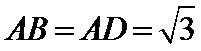
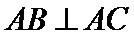
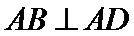
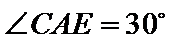
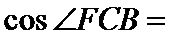
正确答案
17.(12分)
设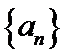
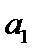
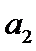
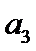
(1) 求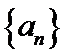
(2) 若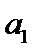
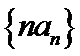
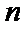
正确答案
解析
18.(12分)
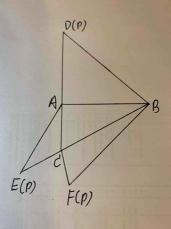
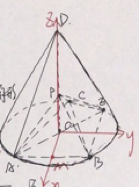
如图,D为圆锥的顶点,O是圆锥底面的圆心,AE为底面直径,AE=AD,
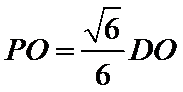
(1)证明:PA⊥平面PBC;
(2)求二面角B-PC-E的余弦值.
正确答案
解析
19. (12分)
甲、乙、丙三位同学进行羽毛球比赛,约定赛制如下:
累计负两场者被淘汰;比赛前抽签决定首先比赛的两人,另一人轮空;每场比赛的胜者与轮空者进行下一场比赛,负者下一轮轮空,直至有一人被淘汰;当一人被淘汰后,剩余的两人继续比赛,直至其中一人被淘汰,另一人最终获胜,比赛结束.
经抽签,甲、乙首先比赛,丙轮空. 设每场比赛双方获胜的概率都为
(1) 求甲连胜四场的概率;
(2) 求需要进行第五场比赛的概率;
(3) 求丙最终获胜的概率.
正确答案
20.(12分)
已知
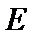
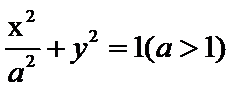
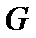
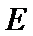
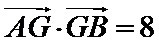
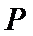
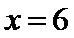
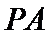
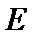
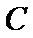
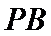
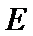
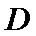
(1)求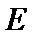
(2)证明:直线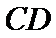
正确答案
21.(12分)
已知函数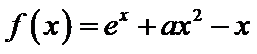
(1) 当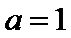
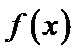
(2) 当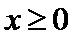
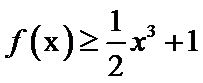
正确答案
(二)选考题:共10分,请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分。
22. [选修4-4:坐标系与参数方程] (10分)
在直角坐标系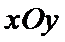
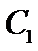
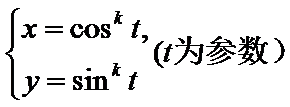
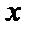
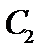
(1) 当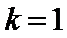
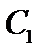
(2) 当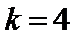
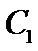
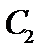
23. [选修4—5:不等式选讲](10分)
已知函数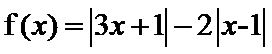
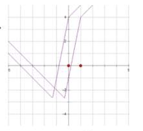
(1) 画出y=f(x)的图像;
(2) 求不等式f(x)>f(x+1)的解集.