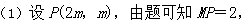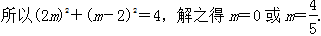- 真题试卷
- 模拟试卷
- 预测试卷
4.若某空间几何体的三视图如图所示,则该几何体的体积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.设平面









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.将函数y=sin的图象上各点的横坐标伸长到原来的3倍,再向右平移个单位,得到的函数的一个对称中心是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若复数z满足z(2-i)=11+7i ,则z为 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.集合
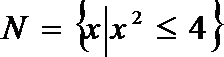
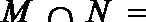
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.在△ABC中,已知角A,B,C所对的边依次为a,b,c,且2lg sin B=lg sin A+lg sin C,则两条直线l1:xsin2A+ysin A=a与l2:xsin2B+ysin C=c的位置关系是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 函数f(x)在定义域R内可导,若f(x)=f(2-x),且当x∈(-∞,1)时,(x-1)·f′(x)<0,设a=f(0),b=f,c=f(3),则( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.若
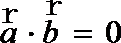
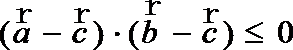

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知命题p:“若x=1且y=2,则x+y=3”,则命题p的否命题为_______________ 。
正确答案
若x≠1或y≠2,则x+y≠3
解析
解析已在路上飞奔,马上就到!
知识点
15.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为线段AA1,B1C上的点,则三棱锥D1-EDF的体积为____________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知函数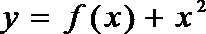
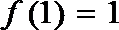
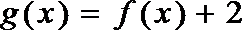
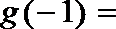
正确答案
-1
解析
解析已在路上飞奔,马上就到!
知识点
17.如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M。
(1)求证:AM⊥PD;
(2)求直线CD与平面ACM所成的角的余弦值。
正确答案
(1)证明:∵PA⊥平面ABCD,
AB⊂平面ABCD,∴PA⊥AB.
∵AB⊥AD,AD∩PA=A,AD⊂平面PAD,
PA⊂平面PAD,∴AB⊥平面PAD.
∵PD⊂平面PAD,∴AB⊥PD,
∵BM⊥PD,AB∩BM=B,AB⊂平面ABM,
BM⊂平面ABM,∴PD⊥平面ABM.
∵AM⊂平面ABM,∴AM⊥PD.
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数
(I)当

(II)若在区间



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知斜三棱柱ABC-A1B1C1中,∠BCA=90°,AC=BC=2,A1在底面ABC上的射影恰为AC的中点D,又知BA1⊥AC1.
(1)求证:AC1⊥平面A1BC;
(2)求C1到平面A1AB的距离;
(3)求二面角A-A1B-C的余弦值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知圆M的方程为x2+(y-2)2=1,直线l的方程为x-2y=0,点P在直线l上,过点P作圆M的切线PA,PB,切点为A,B。
(1)若∠APB=60°,试求点P的坐标;
(2)若P点的坐标为(2,1),过P作直线与圆M交于C,D两点,当CD=时,求直线CD的方程;
(3)求证:经过A,P,M三点的圆必过定点,并求出所有定点的坐标。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 已知a,b,c分别为△ABC的三个内角A,B,C的对边,
(1)求A;
(2)若a=2,△ABC的面积为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知向量






(1) 求函数
(2) 若



正确答案
解析
解析已在路上飞奔,马上就到!