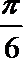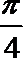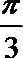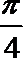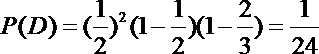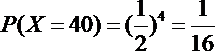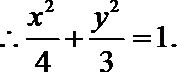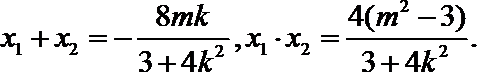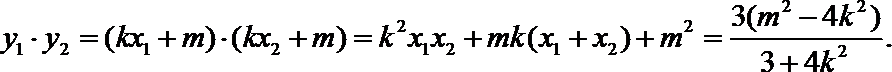- 真题试卷
- 模拟试卷
- 预测试卷
2.设复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知向量a与向量b满足|a|=1,|b|=2,a⊥(b-a),则a 与b的夹角是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.在△ABC中,角A,B,C所对的边长分别为a,b,c,且sin A, sin B,sin C成等比数列,c=2a,则cos B的值为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.执行图所示的程序框图,输出的a的值为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设偶函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.全集U=R,

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知变量x,y满足约束条件

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在直三棱柱


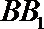

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知双曲线







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.在二项式在二项式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.若直线


正确答案
9
解析
解析已在路上飞奔,马上就到!
知识点
15.某几何体的三视图如图所示,则该几何体的体积为___________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.将容量为n的样本中的数据分成6组,绘制频率分布直方图. 若第一组至第六组数据的频率之比为2∶3∶4∶6∶4∶1,且前三组数据的频数之和等于27,则n等于___________。
正确答案
60
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数




正确答案
c > a > b
解析
解析已在路上飞奔,马上就到!
知识点
17.已知数列

(1)求数列
(2)设


正确答案
解:
(1)当

当


②-①得


(2)

解析
解析已在路上飞奔,马上就到!
知识点
19.如图,正方形ADEF与梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD,AB=AD=
(1)当点M是EC中点时,求证:BM∥平面ADEF;
(2)当EM=2MC时,求平面BDM与平面ABF所成锐二面角的余弦值.
正确答案
解:
(1)以

则



(2)当EM=2MC时,


设面


令



∴平面BDM与平面ABF所成锐二面角的余弦值为
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数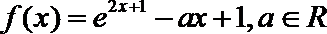
(1)若曲线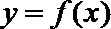
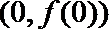
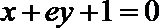
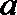
(2)求函数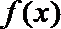
(3)设

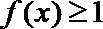
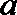
正确答案
解:
(1)由已知得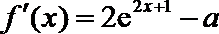
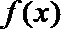

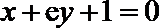
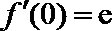
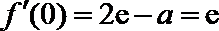

(2)函数


(1)当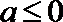

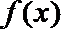

(2)当
令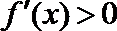
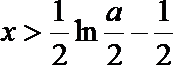
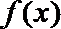
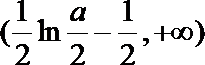
令
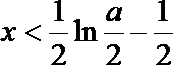
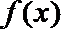

综上所述,当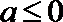
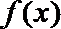
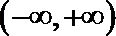
当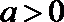
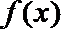


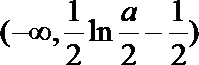
(3)当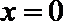

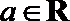
“当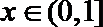
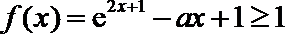
等价于“当

设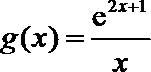
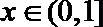


令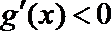
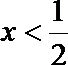
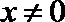
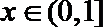
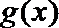

令

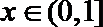
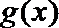
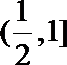
所以函数
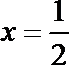

所以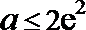

所以实数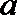
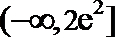
解析
解析已在路上飞奔,马上就到!
知识点
18.2014年全国网球赛规定:比赛分四个阶段,只有上一阶段的胜者,才能继续参加下一阶段的比赛,否则就被淘汰,选手每闯过一个阶段,个人积10分,否则积0分.甲、乙两个网球选手参加了此次比赛.已知甲每个阶段取胜的概率为

(1)求甲、乙两人最后积分之和为20分的概率;
(2)设甲的最后积分为X,求X的分布列和数学期望.
.
正确答案
解:
(1)设“甲、乙两人最后积分之和为20分”为事件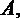
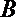

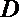
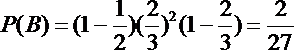

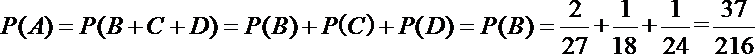
(2)X的取值可为: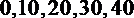
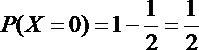
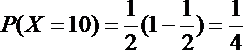
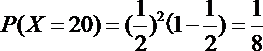
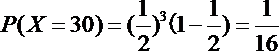
所以X的分布列可为
数学期望
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知椭圆C的中心在坐标原点,焦点在x轴上,椭圆C上的点到焦点距离的最大值为3,最小值为1.
(1)求椭圆C的标准方程;
(2)若直线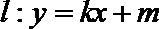
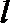
正确答案
解:
(1)由题意设椭圆的标准方程为

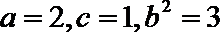
(2)设

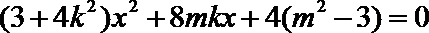


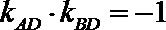
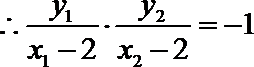



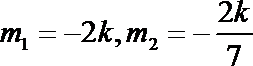

当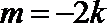

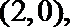
当
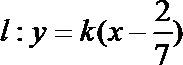
综上可知,直线
解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.
22.选修4-1:几何证明选讲
如图,已知AB是圆O的直径,C为圆O上一点,CD⊥AB于点D,弦BE与CD,AC分别交于点M,N,且MN=MC.
(1)求证:MN=MB;
(2)求证:OC⊥MN.
23.选修4-4:坐标系与参数方程
在直角坐标系xOy中,曲线



24.选修4-5:不等式选讲
已知函数
(1)若


(2)当

正确答案
22.
(1)连接AE,BC,∵AB是圆O的直径,∴∠AEB=90°,∠ACB=90°.
∵MN=MC, ∴∠MCN=∠MNC.
又∵∠ENA=∠MNC, ∴∠ENA=∠MCN,∴∠EAC=∠DCB.
∵∠EAC=∠EBC, ∴∠MBC=∠MCB,∴MB=MC. ∴MN=MB.
(2)设OC∩BE=F,∵OB=OC,∴∠OBC=∠OCB.
由(1)知,∠MBC=∠MCB,∴∠DBM=∠FCM.
又∵∠DMB=∠FMC,∴∠MDB=∠MFC
即∠MFC=90°.∴OC⊥MN.
23.
24.
解析
解析已在路上飞奔,马上就到!