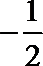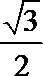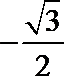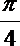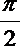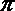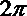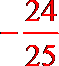- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合M= 


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知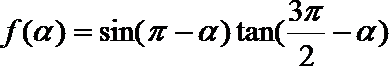
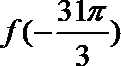
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.函数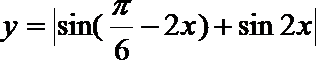
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若函数y=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.定义在






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知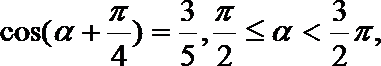
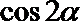
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.当

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.设曲线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.若函数



正确答案

解析
解析已在路上飞奔,马上就到!
知识点
15.
正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
17. 设集合A(p,q)= 


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.
正确答案
(1)设h(x)=m(x2+3x)+n(3x+4)=mx2+3(m+n)x+4n,
∵h(x)是偶函数,
∴m+n=0,∴h(2)=4m+4n=0
(2)设h(x)=2x2+3x-1=m(x2+ax)+n(x+b)=mx2+(am+n)x+nb
∴
{m=2am+n=3nb=-1得 {a=3-n2b=-1n
∴a+2b= 

由ab≠0知,n≠3,
∴a+2b∈ (-∞,-1/2)∪(7/2,+∞)
(3)设h(x)=mlog4(4x+1)+n(x-1)
∵h(x)是偶函数,∴h(-x)-h(x)=0,
即mlog4(4-x+1)+n(-x-1)-mlog4(4x+1)-n(x-1)=0
∴(m+2n)x=0得m=-2n
则h(x)=-2nlog4(4x+1)+n(x-1)=-2n[log4(4x+1)- 



∵h(x)有最小值1,则必有n<0,且有-2n=1∴m=1.n= -12
∴h(x)=log4(2x+ 
h(x)在[0,+∞)上是增函数,在(-∞,0]上是减函数
解析
解析已在路上飞奔,马上就到!
知识点
18.己知集合

(1)求
(2)若
正确答案
(1) 

(2)因而
解析
解析已在路上飞奔,马上就到!
知识点
19.把函数



(1)求
(2)求函数
正确答案
(1)
函数
解析
解析已在路上飞奔,马上就到!
知识点
20.在ΔABC中,已知角A、B、C所对边分别为a、b、c,且满足b2=ac
(1)求证:
(2)求函数
正确答案
(1)∵


又∵
∴
(2)


∴y的值域为
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数
(1)是否存在实数




(2)如果当


正确答案


(1)若




则
∴

当


当


(2)
△=
若△






解析
解析已在路上飞奔,马上就到!