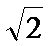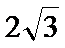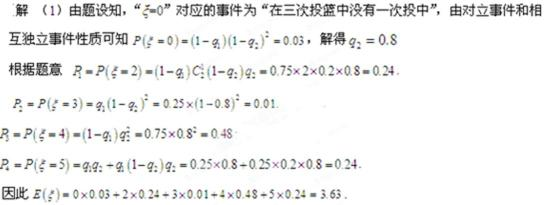- 真题试卷
- 模拟试卷
- 预测试卷
1． 若复数
A7
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
2． 已知集合
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
3． 如果函数
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
4． 以下四个命题中：
①从匀速传递的产品生产流水线上，质检员每10分钟从中抽取一件产品进行某项指标检测，这样的抽样是分层抽样；
②两个随机变量的线性相关性越强，相关系数的绝对值越接近于1；
③某项测量结果ξ服从正态分布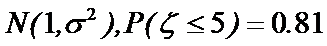
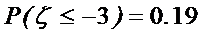
④对于两个分类变量X与Y的随机变量k2的观测值k来说，k越小，判断“X与Y有关系”的把握程度越大．
以上命题中其中真命题的个数为（ ）
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
6． 在△ABC中，角A,B,C的对边分别为
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
9．已知二面角α—l—β为60°，动点P、Q分别在面α、β内，P到β的距离为
A
B2
C
D4
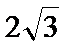
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
5． 
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
7．已知
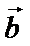
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
8．等比数列{
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
10．若
A
B1
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
11．已知
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
12．已知椭圆
A
B
C
D
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
13．设变量x，y满足约束条件
正确答案
2
解析
解析已在路上飞奔，马上就到！
知识点
15．已知圆C：
正确答案
6
解析
解析已在路上飞奔，马上就到！
知识点
14．在某班进行的演讲比赛中，共有5位选手参加，其中3位女生，2位男生．如果2位男生不能连着出场，且女生甲不能排在第一个，那么出场顺序的排法种数为__________。
正确答案
60
解析
解析已在路上飞奔，马上就到！
知识点
16．已知集合M={(x,y)|y=f(x)}，若对于任意
①
②
③
④
期中是“垂直对点集”的序号是_________。
正确答案
②④
解析
解析已在路上飞奔，马上就到！
知识点
19．在斜三棱ABC-A1B1C1中，侧面ACC1A1⊥面ABC，
（1）求证：CD⊥面ABB1A1；
（2）在侧棱BB1上确定一点E，使得二面角E-A1C1-A的大小为
正确答案
解：（1）∴面ACC1A1⊥面ABC，AB⊥AC
∴AB⊥面ACC1A1，即有AB⊥CD；
又AC=A1C，D为AA1中点，则CD⊥AA1 ∴CD⊥面ABB1A1
（2）
如图所示以点C为坐标系原点，CA为x轴，过C点平行于AB的直线为y轴，
CA1为z轴，建立空间直角坐标系C-xyz，则有A(a,0,0),B(a,a,0),A1(0,0,a), B1(0,a,a)
C1(-a,0,a)，设
即有
所以E点坐标为
由条件易得面A1C1A的一个法向量为
设平面EA1C1的一个法向量为
由
令y=1，则有
则
∴当
解析
解析已在路上飞奔，马上就到！
知识点
20．在某学校组织的一次篮球定点投篮训练中，规定每人最多投3次：在A处每投进一球得3分，在B处每投进一球得2分；如果前两次得分之和超过3分即停止投篮，否则投第三次。某同学在A处的命中率q1为0．25，在B处的命中率为q2，该同学选择先在A处投一球，以后都在B处投，用ξ表示该同学投篮训练结束后所得的总分，其分布列为
（1）求随机变量ξ的数学期望E(ξ)；
（2）试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小。
正确答案
（2）用C表示事件“该同学选择第一次在A处投，以后都在B处投，得分超过3分”，
用D表示事件“该同学选择都在B处投，得分超过3分”，
则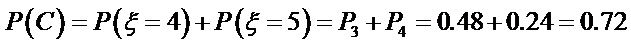
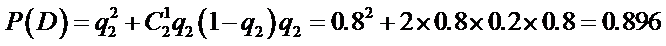
故P(D)>P(C).
即该同学选择都在B处投篮得分超过3分的概率大于该同学选择第一次在A处投以后都在B处投得分超过3分的概率。
解析
解析已在路上飞奔，马上就到！
知识点
17．已知函数
（I）求函数
（Ⅱ）求函数
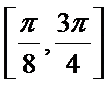
正确答案
解析
解析已在路上飞奔，马上就到！
知识点
18．函数f(x)对任意x∈R都有
（1）数列{an}满足：
（2）令
正确答案
解：（1）令
由
两式相加得：
∴
（2）
∴
解析
解析已在路上飞奔，马上就到！
知识点
21．如图，分别过椭圆E：
（1）求椭圆E的方程；
（2）是否存在点M、N，使得
正确答案
解：（1）当l1与x轴重合时，
∴ l2垂直于x轴，得
得
∴ 椭圆E的方程为
（2）焦点
当直线l1或l2斜率不存在时，P点坐标为(—1，0)或(1，0)．
当直线l1、l2斜率存在时，设斜率分别为
由
∴ 
同理
∵
由题意知
设
由当直线l1或l2斜率不存在时，P点坐标为(—1，0)或(1，0)也满足此方程，
∴
∴ 存在点M、N其坐标分别为
解析
解析已在路上飞奔，马上就到！
知识点
22．已知f(x)=ex-t(x+1)．
（1）若f(x)≥0对一切正实数x恒成立，求t的取值范围；
（2）设
（3）求证：
正确答案
解析
解析已在路上飞奔，马上就到！