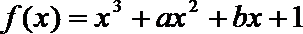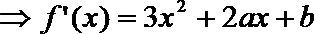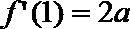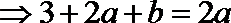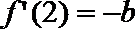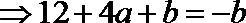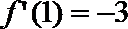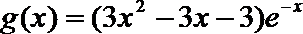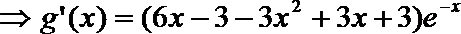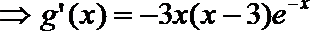- 真题试卷
- 模拟试卷
- 预测试卷
1.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.在




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设集合




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.下列区间中,函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知定义在





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.设函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知向量





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.在直角坐标系








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知点










正确答案
外心、重心、垂心
解析
解析已在路上飞奔,马上就到!
知识点
15.下列几个结论:
①“

②
③已知




④若点



⑤函数
其中正确的是__________(写出所有正确命题的序号)
正确答案
②③④
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数
(1)求
(2)求


正确答案
解:(1)
(2)




且当

解析
解析已在路上飞奔,马上就到!
知识点
19. 设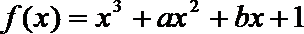
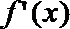
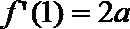
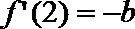
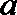
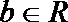
(1)求曲线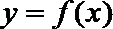
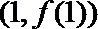
(2)设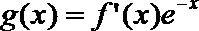
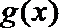
正确答案
解:
(1)
又
所以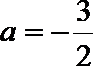
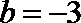
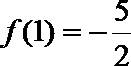
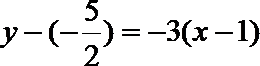
(2)
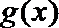
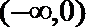
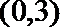
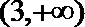
所以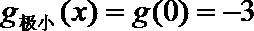
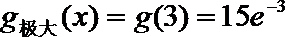
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,在四面体




(1)设




(2)求二面角
正确答案
(1)证明:过


分别以





则




则设





(2)依题意有:面


设面
由
即
由于二面角
所以二面角

解析
解析已在路上飞奔,马上就到!
知识点
17.在







(1)求角
(2)若


正确答案
解:
(1)

(2)由

解析
解析已在路上飞奔,马上就到!
知识点
20. 设


(1)求函数
(2)若

正确答案
解:
(1)
由


函数

函数

(2)由于
即



解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数

(1)讨论函数
(2)如果存在



(3)如果对任意



正确答案
解:
(1)
①当




②当





(2)存在


等价于

当


由上表可知:

所以满足条件的最大整数
(3)当

等价于
记



当


即函数

当


即函数




所以
解析
解析已在路上飞奔,马上就到!