- 真题试卷
- 模拟试卷
- 预测试卷
已知抛物线

正确答案
解析
略
知识点
1. 已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知



“
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知某个三棱锥的三视图如右,根据图中标出的尺寸
(单位:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.如图,函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知点



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.点


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知点





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.给出以下四个命题:
① 过点



② 当

③ 



④“


其中正确命题的个数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知双曲线



正确答案
48
解析
解析已在路上飞奔,马上就到!
知识点
15.一圆与两坐标轴分别相交于A、B、C、D四个交点,若A、B、C三个点都在函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若实数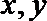
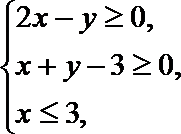
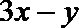
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
12.设等比数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.设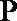
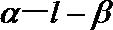
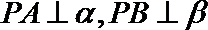
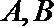
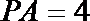
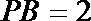
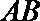
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 在直角坐标系


(1)求圆
(2)过点





正确答案
(1)令圆



∴圆

(2)由题得:




若


若




∴ 
∴ 
综上可知,直线


解析
解析已在路上飞奔,马上就到!
知识点
16. 在





(1)求
(2)求
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知数列



(1)求

(2)若数列

正确答案
(1)∵


解析
解析已在路上飞奔,马上就到!
知识点
19.如图,在五面体







(1)求异面直线

(2)证明:平面

(3)求二面角
正确答案
(3)解:设平面
于是
又由题设,平面
解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆的焦点在






(1)求椭圆的标准方程;
(2)设点



(3)设点








正确答案
(1)设椭圆方程为
故椭圆方程为
解析
解析已在路上飞奔,马上就到!