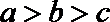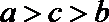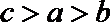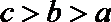- 真题试卷
- 模拟试卷
- 预测试卷
4.下列函数中,在区间
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知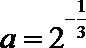
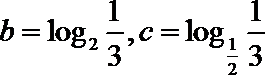
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知命题

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.直线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.设函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.“

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设




①
②
③
④当
其中正确的命题的序号是________。
正确答案
①②④
解析
解析已在路上飞奔,马上就到!
知识点
15.已知随机变量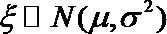
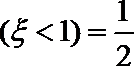
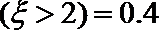
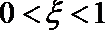
正确答案
0.1
解析
解析已在路上飞奔,马上就到!
知识点
13.将5位志愿者分成3组,其中两组各2人,另一组1人,分赴青奥会的三个不同场馆服务,不同的分配方案有 _______种(用数字作答)
正确答案
90
解析
解析已在路上飞奔,马上就到!
知识点
14.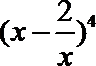
正确答案
24
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)设

(2)若f(1)=0,函数
正确答案
(1)由f(x)=ex-ax2-bx-1,得g(x)=f′(x)=ex-2ax-b.
所以g′(x)=ex-2a.
当x∈[0,1]时,g′(x)∈[1-2a,e-2a].
当a≤
因此g(x)在[0,1]上的最小值是g(0)=1-b;
当a≥
因此g(x)在[0,1]上的最小值是g(1)=e-2a-b;
当

所以函数g(x)在区间[0,ln(2a)]上单调递减,在区间(ln(2a),1]上单调递增,
于是,g(x)在[0,1]上的最小值是g(ln(2a))=2a-2aln(2a)-b.
综上所述,当a≤
当

当a≥
g(1)=e-2a-b
(2)设x0为f(x)在区间(0,1)内的一个零点,
则由f(0)=f(x0)=0可知
f(x)在区间(0,x0)上不可能单调递增,也不可能单调递减.
则g(x)不可能恒为正,也不可能恒为负.
故g(x)在区间(0,x0)内存在零点x1.
同理g(x)在区间(x0,1)内存在零点x2.
故g(x)在区间(0,1)内至少有两个零点.
由(1)知,当a≤
故g(x)在(0,1)内至多有一个零点;
当a≥
故g(x)在(0,1)内至多有一个零点,都不合题意.
所以

此时g(x)在区间[0,ln(2a)]上单调递减,在区间(ln(2a),1]上单调递增.
因此x1∈(0,ln(2a)],x2∈(ln(2a),1),必有
g(0)=1-b>0,g(1)=e-2a-b>0.
由f(1)=0得a+b=e-1<2,
则g(0)=a-e+2>0,g(1)=1-a>0,
解得e-2<a<1.
当e-2<a<1时,g(x)在区间[0,1]内有最小值g(ln(2a)).
若g(ln(2a))≥0,则g(x)≥0(x∈[0,1]),
从而f(x)在区间[0,1]内单调递增,这与f(0)=f(1)=0矛盾,所以g(ln(2a))<0.
又g(0)=a-e+2>0,g(1)=1-a>0.
故此时g(x)在(0,ln(2a))和(ln(2a),1)内各只有一个零点x1和x2.
由此可知f(x)在[0,x1]上单调递增,在(x1,x2)上单调递减,在[x2,1]上单调递增.
所以f(x1)>f(0)=0,f(x2)<f(1)=0,
故f(x)在(x1,x2)内有零点.
综上可知,a的取值范围是(e-2,1).
故g(x)≤0,即f(x)≤2x-2.
解析
解析已在路上飞奔,马上就到!
知识点
22.请考生在下列三题中任选择一题作答,如果多做,则按所作的第一题计分。
1.如图,

(Ⅰ)证明:

(Ⅱ)若


2.以直角坐标系的原点




(I)求直线
(II)试判定直线
3.已知函数
(I) 解关于
(II)若函数


正确答案
1.
证明:(Ⅰ)由已知条件,可得∠BAE=∠CAD.
因为∠AEB与∠ACB是同弧上的圆周角,所以∠AEB=∠ACD.
故△ABE∽△ADC.
(Ⅱ)因为△ABE∽△ADC,所以
又S=

则sin∠BAC=1,又∠BAC为三角形内角,
所以∠BAC=90°.
2.
(1)直线

M点的直角坐标为(0,4) 圆C半径
图C方程 

代入得圆C极坐标方程 
(2)直线
圆心M到
∴直线
3.
(1)
当
当

∴不等式解集为(

(2)

设
做出



图象在
解析
解析已在路上飞奔,马上就到!
知识点
17.设命题p:实数x满足




(1)若


(2)若

正确答案
(1)当


又


由
所以实数
(2) 因为

所以

又

所以
所以实数

解析
解析已在路上飞奔,马上就到!
知识点
18.某市公租房的房源位于
(1)恰有2人申请
(2)申请的房源所在片区的个数
正确答案
(1)解:所有可能的申请方式有

从而恰有2人申请A片区房源的概率为
(2)的所有取值为1、2、3
所以
解析
解析已在路上飞奔,马上就到!
知识点
20.为加快新能源汽车产业发展,推进节能减排,国家对消费者购买新能源汽车给予补贴,其中对纯电动乘用车补贴标准如下表:
某校研究性学习小组,从汽车市场上随机选取了

(1)求



(2)若从这



(3)若以频率作为概率,设


正确答案
(1)M=10,x=0.5,y=3,z=0.3
(2)设该事件为事件A,则
(3)X的可能取值为3.5、5、6
解析
解析已在路上飞奔,马上就到!
知识点
19.设函数

(1)求a,b的值;
(2)证明:
正确答案
由题设,y=f(x)在点P(1,0)处切线的斜率为2.
∴
因此实数a,b的值分别为-1和3.
(2)证明 f(x)=x-x2+3ln x(x>0).
设g(x)=f(x)-(2x-2)=2-x-x2+3ln x,
则g′(x)=-1-2x+

当0<x<1时,g′(x)>0;当x>1时,g′(x)<0.
∴g(x)在 (0,1)上单调递增;在(1,+∞)上单调递减.
∴g(x)在x=1处有最大值g(1)=0,
∴f(x)-(2x-2)≤0,即f(x)≤2x-2,得证
解析
解析已在路上飞奔,马上就到!