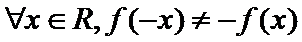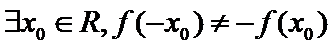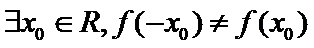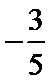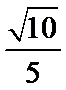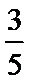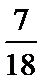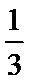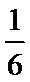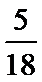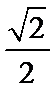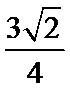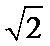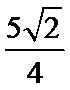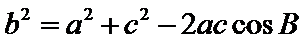- 真题试卷
- 模拟试卷
- 预测试卷
4.

正确答案
解析






考查方向
解题思路
1.先写出

易错点
1.展开式中的通项公式易丢掉-1导致错选D;2.对于通项公式的化简即指数幂的运算出错。
知识点
1.已知集合

正确答案
解析



考查方向
解题思路
1.先分别将集合A,B化简;2.利用数轴求两个集合的交集。
易错点
对于集合A的理解不到位,导致理解成y的范围致错。
知识点
2.设复数z满足

正确答案
解析
由


考查方向
解题思路
1.先利用复数的运算化简z;2.求出复数z的共轭复数即可得到答案。
易错点
1。不知道共轭复数的概念导致出错;2复数运算出错。
知识点
3.设
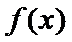
正确答案
考查方向
解题思路
1.先根据奇函数的定义得到题中命题的逆否命题;
易错点
1.全称命题的否定形式写错;2.不能正确理解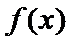
知识点
5.一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了4次试验,收集数据如表示:根据右表可得回归方程

正确答案
解析
由题中给出的表格得





考查方向
解题思路
1.先求出样本点的中心

易错点
1.不知道回归直线过样本点的中心,误将表格中的点带入回归直线导致出错2.运算结果出错。
知识点
6.已知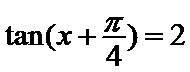
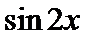
正确答案
解析
由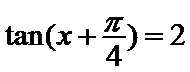
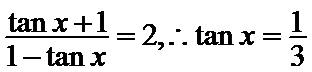
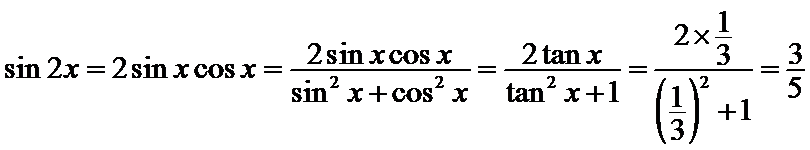
考查方向
解题思路
1.先利用两角和的正切公式求出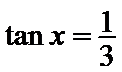
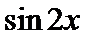
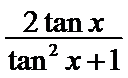
易错点
1. 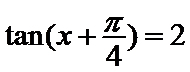
知识点
7.执行如图1的程序框图,则输出S的值为()
正确答案
解析








考查方向
解题思路
根据给出的程序框图循环执行,后发现S是以4为周期的循环结构,然后发现2016与4的关系后可以选出正确选项.
易错点
无法确定程序结束的条件导致出错,容易误选D.
知识点
8.若以连续掷两次骰子分别得到的点数
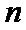
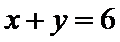
正确答案
解析
以连续掷两次骰子分别得到的点数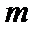
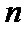

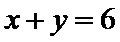
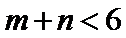
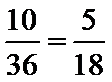
考查方向
解题思路
1.先求出以连续掷两次骰子分别得到的点数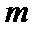
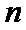
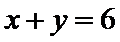
易错点
1.不会计算连续掷两次骰子共有多少种情况;2.不会求点P在直线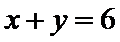
知识点
9.若x、y满足

正确答案
解析





考查方向
解题思路
1.先做出约束条件对应的可行域;2.求出可行域端点的坐标,将各个点带入目标函数z的最大值和最小值即可。
易错点

知识点
12.已知直线



正确答案
解析
由已知得圆心到直线的距离小于半径,即
【或由
所以
由

如图,又由
因



考查方向
解题思路
1.先根据直线


易错点
不会转化题中向量的条件,导致无法做出正确答案。
知识点
10.双曲线








正确答案
解析
由题意知:






考查方向
解题思路
1.先根据题意求出M点到坐标;2.根据直线



易错点
1.不会求M点的坐标;
2.不会转化题中的倾斜角为45度。
知识点
11.已知函数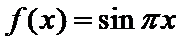
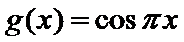
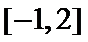
正确答案
解析
由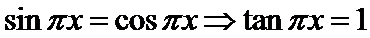
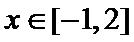
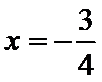
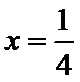
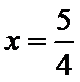
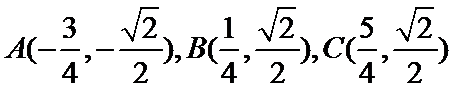
故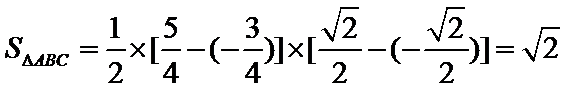
考查方向
解题思路
1.先根据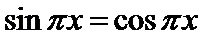
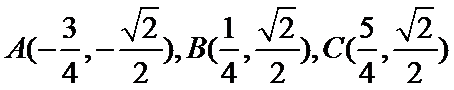
易错点
1.不会结合图像求出A,B,C的坐标;2.不会做函数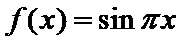
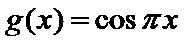
知识点
13.已知

正确答案
.
解析


考查方向
解题思路
1.先根据向量

易错点
运算会出错或不会求向量
知识点
14.已知函数




正确答案
1
解析
由函数


故
考查方向
解题思路
1.利用函数




易错点
1.不会将

知识点
15.某组合体的三视图如图2示,则该几何体的体积为 .
正确答案

解析
依题意知,该几何体是上面长方体下接半圆柱的组合体,故其体积
为:
考查方向
解题思路
1.先根据三视图还原成原来的几何体;2.根据体积公式求出该几何体的体积。
易错点
1.不会根据三视图还原原来的几何体形状;
2.记不住圆柱的体积公式导致结果出错。
知识点
16.已知△ABC中,角A、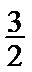
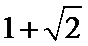

正确答案
2
解析
∵A、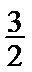
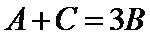
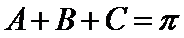
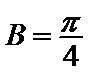
由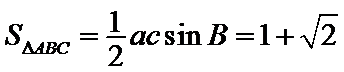
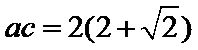
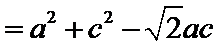
及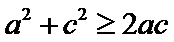
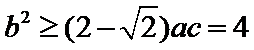
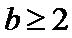
考查方向
解题思路
1.先根据条件A、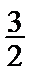
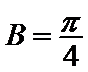
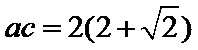
易错点
1.不会转化题中的条件A、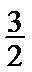

知识点
已知数列




17.求数列
18.设




正确答案
(1)
解析
(Ⅰ)当


当


显然当
∴
考查方向
解题思路
先令



易错点
1.不会转化题中的条件

正确答案
(2)
解析
(Ⅱ)∵
∴
考查方向
解题思路
由第(1)问的结果可以得到
易错点
不明白
某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得
19.根据以上资料完成下面的2×2列联表,若据此数据算得
20.以此“满意”的频率作为概率,求在3人中恰有2人满意的概率;
21.从以上男性用户中抽取2人,女性用户中抽取1人,其中满意的人数为

正确答案
(1)在犯错的概率不超过5%的前提下,不能认为“满意与否”与“性别”有关;
解析
:(Ⅰ)
∵
∴在犯错的概率不超过5%的前提下,不能认为“满意与否”与“性别”有关。
考查方向
解题思路
先将题中给出的茎叶图处理成列联表,然后带入求得
易错点
将茎叶图处理成列联表数据出错,
在求
正确答案
(2)
解析
(Ⅱ)由频率估计“满意”的概率为
∴在3人中恰有2人满意的概率为

考查方向
解题思路
先求出“满意”的概率,然后利用n次独立重复试验的概率求法求出概率;
易错点
求概率时忘记乘以
正确答案
(3)

数学期望
解析
(Ⅲ)





数学期望
考查方向
解题思路
先求出随机变量的取值和取各个值的概率后利用公式求出其期望。
易错点
不会求随机变量取各个值的概率。
如图4,已知四棱锥P—ABCD中,PA⊥平面ABCD,底面ABCD
中,∠A=90°,AB∥CD,AB=1,AD=CD=2.
22.若二面角P—CD—B为45°,求证:平面

23.在(Ⅰ)的条件下,求点A到平面PBC的距离.
正确答案
(1)略;
解析
Ⅰ)
∵AB//CD,AB⊥AD,∴


∴

取PD的中点E,PC的中点F,连结AE,BF,EF,
则


∴





∴四边形ABFE为平行四边形,∴


∵


考查方向
解题思路
1.先找出


易错点
不会从图形中找到二面角P—CD—B的平面角;
不知道该证明哪条直线垂直于哪个平面;
正确答案
(2)
解析
(Ⅱ)设点A到平面PBC的距离为



考查方向
解题思路
1.先找出


2.利用等体积法直接求解答案即可。
易错点
利用等体积法运算时求解算数出错。
已知




24.求

25.如图5所示,过


(点



正确答案
(1)

解析
(Ⅰ)由点




抛物线的方程为


考查方向
解题思路
1.先利用抛物线定义求出p,然后将点M的坐标带入求解即可;2.设出直线



易错点
不会利用抛物线的定义转化题中的条件



正确答案
(2)略
解析
(Ⅱ):显然直线

分别设


联立

联立

设



则


故

注意到点


故得



考查方向
解题思路
1.先利用抛物线定义求出p,然后将点M的坐标带入求解即可;2.设出直线



易错点
1.不会利用抛物线的定义转化题中的条件



选修4—1:几何证明选讲
如图6,圆O的直径

圆O于点C,D,过点P作AP的垂线,交直线AC于点E,交直线AD于点F.
28. 当

29.求
正确答案
(1)
解析
解:(Ⅰ) 连结BC,∵AB是圆O的直径 ∴则
又

∵
考查方向
解题思路
找不到

易错点
不会使用第(1)问的结论推导第(2)问;
正确答案
(2)24;
解析
(Ⅱ)由(Ⅰ)知
∴D、C、E、F四点共圆,
∴
∵PC、PA都是圆O的割线,∴
∴
考查方向
解题思路
无法发现D、C、E、F四点共圆导致不能使用割线定理。
易错点
不会使用第(1)问的结论推导第(2)问;
设函数

26.若

27.若函数
正确答案
(1)

解析
(Ⅰ)
由x = e是f(x)的极值点,得


经检验,符合题意,所以

考查方向
解题思路
求导后根据

易错点
不会转化


正确答案
(2)
解析
(Ⅱ)由已知得方程
即曲线f(x)与直线
易知

①当

②当


∴

当


同理f(x)在


又极大值
③当a>1时,

∴



可得f(x) 在



又


所以


由


所以
综上知,
考查方向
解题思路
先将题意转化为求函数

易错点
不会转化