- 真题试卷
- 模拟试卷
- 预测试卷
7.已知圆








正确答案
解析
圆C








考查方向
解题思路
1.先求出圆

易错点
圆

知识点
9.某空间几何体的三视图如图所示,则该几何体的外接球的表面积是( )
正确答案
解析
由三视图可知,该几何体为直三棱柱,高为4,底面为等腰三角形,底长为



考查方向
解题思路
1.先根据三视图还原原来的几何体;2.找到几何体外接球的球心在中界面的外心处,然后利用几何图形求解。
易错点
1.不能根据三视图还原原来的几何体;2.不会确定几何体外接球的球心在什么位置。
知识点
10.若





正确答案
解析
由















考查方向
解题思路
1.先根据题中给出的条件求出函数

易错点
1.三角函数的基础知识记不住导致出错;2.不考虑函数的单调性直接将0,
知识点
2.已知复数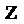
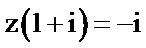
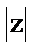
正确答案
解析
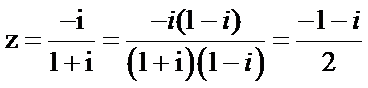
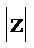
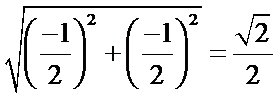
考查方向
解题思路
1.先利用复数的运算法则化简复数;2.根据复数的模的公式即可得到答案。
易错点
复数运算出错。
知识点
3.在等比数列



正确答案
解析
由




考查方向
解题思路
先利用等比数列的性质求出


易错点
易直接利用基本量得到关于首相和公比的方程组解方程出错,误选B。
知识点
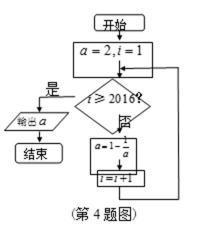
4.如图所示的程序框图的运行结果为( )
正确答案
解析
第1次运算: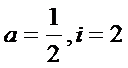
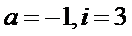
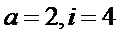
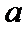
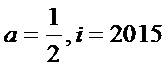
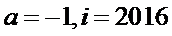

考查方向
解题思路
根据给出的程序框图循环执行,后发现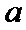
易错点
不知道当条件满足退出循环时a的值是多少或循环到什么时候停出错。
知识点
5.在区间


正确答案
解析
由



考查方向
解题思路
先求出正方形的面积为16,再求围成的梯形的面积为
易错点
不理解题中给出的二维模型,导致无法入手。
知识点
6.在平行四边形ABCD中,




正确答案
解析



考查方向
解题思路
1.先将向量


易错点
不知道应该将向量


知识点
8.已知函数


正确答案
解析






考查方向
解题思路
先根据函数


易错点
1.函数
知识点
1.已知集合

正确答案
解析
由题意得


考查方向
解题思路
1.先将集合A,B化简;2.利用数轴求出
易错点
.不理解集合B表示什么导致出错。
知识点
11.已知





正确答案
解析
由题意知,










考查方向
解题思路
1.先根据题意构造函数

易错点
1.不会构建函数

知识点
12.已知函数





正确答案
解析


(1)当



(2)当













考查方向
解题思路
1.先求导后判断导数的正负,2.当导数有正有负时转化为一元二次方程根的分布处理,接着转化为线性规划使得问题得以解决。
易错点
1.不知道题中的条件:函数



知识点
14.若

正确答案
解析
由基本不等式得



考查方向
解题思路
利用基本不等式得到
易错点
找不到

知识点
15.已知



正确答案
2
解析
由题意得








考查方向
解题思路
1.先根据题意先表示出


易错点
1.点(m,n)的坐标求错;2.不会建立关于a,b,c之间的关系。
知识点
16.数列







正确答案
7280
解析
由






考查方向
解题思路
1.先根据



易错点
1.不会将

知识点
13.已知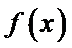
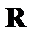
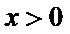
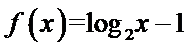
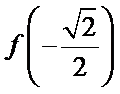
正确答案
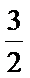
解析

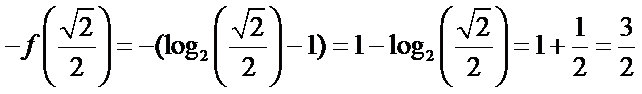
考查方向
解题思路
先利用奇偶性将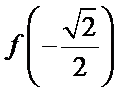
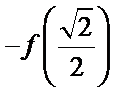
易错点
1.不会利用奇偶性将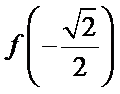
知识点
如图,在平面四边形





17.求
18.求
正确答案
(1) 
解析
(Ⅰ)在

即


由正
考查方向
解题思路
先利用余弦定理求出
易错点
不知道该在哪个三角形中使用什么定理;
正确答案
;(2)
解析
(Ⅱ)由(Ⅰ)有:

所以
由正弦定理得:
考查方向
解题思路
利用第(1)问的结论求出
易错点
意识不到
国内某知名大学有男生14000人,女生10000人.该校体育学院想了解本校学生的运动状况,根据性别采取分层抽样的方法从全校学生中抽取120人

男生平均每天运动的时间分布情况:
女生平均每天运动的时间分布情况:
19.请根据样本估算该校男生平均每天运动的时间(结果精确到
20.若规定平均每
为“非运动达人”.
①请根据样本估算该校“运动达人”的数量;
②请根据上述表格中的统计数据填写下面
误的概率不超过
参考公式:
参考数据:
正确答案
(1) 
解析
(Ⅰ)由分层抽样得:男生抽取的人数为




则该校男生平均每天运动的时间为:

故该校男生平均每天运动的时间约为
考查方向
解题思路
根据题中给出的数据估计该校男生平均每天运动的时间约为
易错点
不会根据频率分布直方图估计平均数;
正确答案
(2) ①4000;
②

解析
(Ⅱ)①样本中“运动达人”所占比例是

②由表格可知:
故
故在犯错误的概率不超过
考查方向
解题思路
先列出列联表后计算
易错点
处理数据列
如图,在三棱柱




21.求证:

22.当三棱锥



正确答案
(1)略
解析
(Ⅰ)连结















考查方向
解题思路
先证明
易错点
找不到
正确答案
(2)
解析
(Ⅱ)设点








由(Ⅰ)知:





∵




∵













设






考查方向
解题思路
先求三棱锥

易错点
三棱锥

定义:在平面内,点













23.求曲线
24.过原点的直线











正确答案
(1)
解析
(Ⅰ)由分析知:点

所以


设椭圆方程为

所以

考查方向
解题思路
先根据椭圆的定义得到
易错点
找不到
正确答案
(2)
解析
(Ⅱ)设















所以
所以直线




可得
所以
考查方向
解题思路
设出直线

和
易错点
不知该如何入手,运算复杂出错。
已知函数
25.讨论
26.当





正确答案
(1)当






解析
(Ⅰ)函数


当



当





当


∴当






考查方向
解题思路
求导后根据a的范围讨论单调性即可;
易错点
问题中不讨论a的范围导致丢解;
正确答案
(2)
解析
(Ⅱ)当











则

由

记


记

∴



而




∴


而





考查方向
解题思路
先利用第(1)问的结论构造函数

易错点
不会构造函数
4-1 :几何证明选讲








27.求证:

28.若


正确答案
(1)略;
解析
(Ⅰ)连结




而




而


考查方向
解题思路
先证明


易错点
不会做辅助线导致没有思路;
正确答案
(2)5
解析
(Ⅱ)连



设




考查方向
解题思路
先证明

易错点
不会利用圆的内接四边形的性质出错。