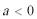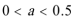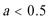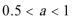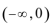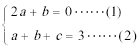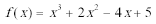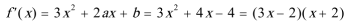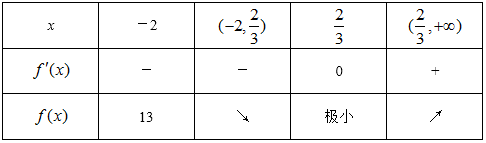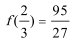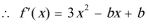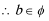- 真题试卷
- 模拟试卷
- 预测试卷
3.已知数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.不等式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.有一条信息, 若1人得知后用1小时将其传给2人, 这2人又用1小时分别传给未知此信息的另外2人, 如此继续下去, 要传遍100万人口的城市, 所需的时间大约是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知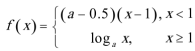
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若关于

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若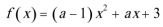
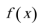
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.观察下表中的数字排列规律,第n行(
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数

(1)求
(2)若



正确答案
解(1) 由题 
(2) 








解方程,得解为1,




解析
解析已在路上飞奔,马上就到!
知识点
18.已知集合A=
(1)若
(2)若
正确答案
解:由已知得:集合A=
(1)因为


(2)
因为


所以
解析
解析已在路上飞奔,马上就到!
知识点
21.若公比为c的等比数列



(1)求c的值;
(2)求数列

正确答案
解:(1)解:由题设,当


由题设条件可得

解得c=1或
(2)解:由(1),需要分两种情况讨论,
当c=1时,数列

这时,数列

当



这时,数列

1 式两边同乘

①式减去②式,得
所以
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数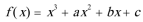
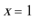
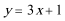
(1)若函数
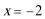

(2)在(1)条件下,若函数
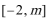

(3)若函数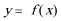
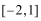
正确答案
解:(1)由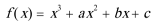

在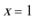
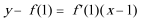
由已知切线方程为
所以: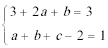
(2)
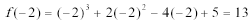
当
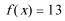


(3)
又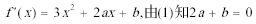
依题意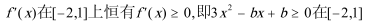
1 在
②在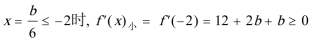
2 在
综合上述讨论可知,所求参数b取值范围是:b≥0
解析
解析已在路上飞奔,马上就到!
知识点
20.如图








(1)若


(2)求
正确答案
解:(1)因为A点的坐标为


所以
(2)因为三角形AOB为正三角形,所以
所以

所以


即
解析
解析已在路上飞奔,马上就到!