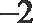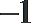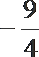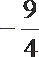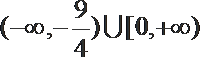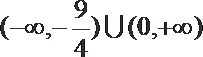理科数学杭州市2011年高三试卷

精品

单选题
填空题
简答题

立即下载

理科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共10小题，每小题5分，共50分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

2．设向量，，则是”的（）

A充分但不必要条件

B必要但不充分条件

C充要条件

D既不充分也不必要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：单选题

分值: 5分

1．等差数列的前项和为，若 ( )

B16

D10

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的基本运算等差数列的性质及应用

题型：单选题

分值: 5分

5．设函数，若，则的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

4．设函数，把的图象向右平移个单位后，图象恰好为函数的图象，则的值可以为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算函数y=Asin（ωx+φ）的图象变换

题型：单选题

分值: 5分

7．已知点P是双曲线右支上一点，分别是双曲线的左、右焦点，I为的内心，若成立，则双曲线的离心率为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：单选题

分值: 5分

3．某班选派6人参加两项志愿者活动，每项活动最多安排4人，则不同的安排方法有（）

A50种

B70种

C35种

D55种

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像与性质

题型：单选题

分值: 5分

6．若实数，满足不等式组且的最大值为9，则实数（）

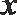
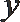
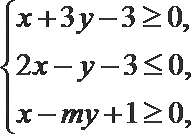
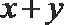
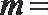
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

一元二次不等式的解法

题型：单选题

分值: 5分

9．如图所示,已知正方体的棱长为2, 长为2的线段的一个端点在棱上运动, 另一端点在正方形内运动, 则的中点的轨迹的面积为( )

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：单选题

分值: 5分

8．如果函数没有零点，则的取值范围为 ( )

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数零点的判断和求解

题型：单选题

分值: 5分

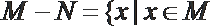
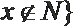
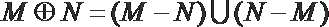
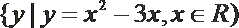
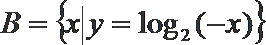
10．对于集合M、N，定义：且，，设＝，，则= （）

A（，0]

B[，0)

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

交、并、补集的混合运算集合中的新定义问题对数函数的定义域

填空题本大题共7小题，每小题4分，共28分。把答案填写在题中横线上。

题型：填空题

分值: 4分

11．．

正确答案

-1

解析

解析已在路上飞奔，马上就到！

知识点

换底公式的应用

题型：填空题

分值: 4分

13．一个几何体的三视图如图所示，则该几何体的体积是（）．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的图像

题型：填空题

分值: 4分

14．已知为如图所示的程序框图中输出的结果，则二项式的展开式中含项的系数是（）．

正确答案

-192

解析

解析已在路上飞奔，马上就到！

知识点

选择结构

题型：填空题

分值: 4分

15．一袋子中有大小、质量均相同的10个小球，其中标记“开”字的小球有5个，标记“心”字的小球有3个，标记“乐”字的小球有2个．从中任意摸出1个球确定标记后放回袋中，再从中任取1个球．不断重复以上操作，最多取3次，并规定若取出“乐”字球，则停止摸球．则摸球次数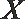的数学期望为（）．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：填空题

分值: 4分

16．如图所示，在直三棱柱ABC－A1B1C1中，底面为直角三角形，∠ACB＝90°，AC＝，BC＝CC1＝1，P是BC1上一动点，则的最小值是_____．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：填空题

分值: 4分

12．已知圆为正实数）上任意一点关于直线的对称点都在圆C上，则的最小值为（）．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 4分

17．如图，在△ABC和△AEF中，B是EF的中点，AB=EF=1，，若，则与的夹角等于（）．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

异面直线及其所成的角

简答题（综合题）本大题共72分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 14分

18．已知向量，函数，且图象上一个最高点的坐标为，与之相邻的一个最低点的坐标为.

（Ⅰ）求的解析式；

（Ⅱ）在△ABC中，是角A、B、C所对的边，且满足，求角B的大小以及的取值范围.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：简答题

分值: 14分

19．已知数列的前n项和满足：（为常数，）

（Ⅰ）求的通项公式；

（Ⅱ）设，若数列为等比数列，求的值；

（Ⅲ）在满足条件（Ⅱ）的情形下，，数列的前n项和为.求证：．

正确答案

（Ⅰ）

∴

当时，

两式相减得：， (a≠0，n≥2)，即是等比数列．

∴；

（Ⅱ）由（Ⅰ）知a≠1

，

若为等比数列，则有

而，

故，

解得，

再将代入得成立，

所以．

（III）证明：由（Ⅱ）知，

所以，

所以

解析

解析已在路上飞奔，马上就到！

知识点

简单复合函数的导数

题型：简答题

分值: 14分

20．如图，在四棱锥中，底面为平行四边形，平面，在棱上．

（Ⅰ）当时，求证平面

（Ⅱ）当二面角的大小为时，求直线与平面所成角的正弦值．

正确答案

（Ⅰ）

在平行四边形中，由，，，

易知，

又平面，所以平面,

∴，

在直角三角形中，易得，

在直角三角形中，，，

又，∴，

可得

．

∴，

又∵，∴平面．

（Ⅱ）由（Ⅰ）可知,,，

可知为二面角的平面角，

，此时为的中点．

过作,连结,则平面平面,

作,则平面,连结,

可得为直线与平面所成的角．

因为,,

所以．

在中，

直线与平面所成角的正弦值大小为．

解法二：

依题意易知，平面ACD．以A为坐标原点，AC、AD、SA分别为轴建立空间直角坐标系，则易得

，

（Ⅰ）由有，

易得，从而平面ACE．

(Ⅱ)由平面，二面角的平面角．

又，则 E为的中点，

即 ,

设平面的法向量为

则，令,得，
从而，

直线与平面所成角的正弦值大小为．

解析

解析已在路上飞奔，马上就到！

知识点

平行关系的综合应用

题型：简答题

分值: 15分

21．已知椭圆的离心率为，以原点为圆心、椭圆的短半轴长为半径的圆与直线相切．

（Ⅰ）求椭圆的方程；

（Ⅱ）若过点(2，0)的直线与椭圆相交于两点，为椭圆上一点，且满足（为坐标原点），当＜时，求实数的取值范围．

正确答案

（Ⅰ）由题意知，所以．即．

又因为，所以，．故椭圆的方程为．

（Ⅱ）由题意知直线的斜率存在．设：，，，，

由得．

，．

，．∵，∴，，．

∵点在椭圆上，∴，∴．

∵＜，∴，∴

∴

，∴，∴．

∴，∵，∴，

∴或，

∴实数取值范围为．

(注意：可设直线方程为，但需要讨论或两种情况)

解析

解析已在路上飞奔，马上就到！

知识点

集合的含义交集及其运算

题型：简答题

分值: 15分

22．已知

（Ⅰ）求函数上的最小值；

（Ⅱ）若对一切恒成立，求实数的取值范围；

（Ⅲ）证明：对一切，都有成立.

正确答案

（Ⅰ），

当单调递减，当单调递增

①，即时，

；

②，即时，上单调递增，；

所以

（Ⅱ），则，

设，则，

① 单调递减， ② 单调递增，

所以，对一切恒成立，所以；

（Ⅲ）问题等价于证明，

由（1）可知的最小值是，当且仅当时取到，

设，则，易知

，当且仅当时取到，

从而对一切，都有成立

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

理科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

理科数学热门试卷