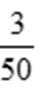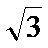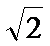- 真题试卷
- 模拟试卷
- 预测试卷
1. 某学校有男学生400名,女学生600名.为了解男女学生在学习兴趣与业余爱好方面是否存在显著差异,拟从全体学生中抽取男学生40名,女学生60名进行调查,则这种抽样方法是( )
正确答案
解析
抽签法是指在总体中,随机抽取,所以A选项不对,随机数法和抽签法类似,属于简单随机抽样法,B选项也不对,C选项中,系统抽样法是指将总体均匀分成几个部分,按照事先确定的规则在各部分抽取,而本题中,没有均匀分层,所以应该算是分层抽样法,所以答案是D.
考查方向
解题思路
根据题意,结合常见抽样方式特点直接可以判断,题目中的抽样方法是属于分层抽样法。
易错点
常用的抽样方法及各自方法的特点
知识点
2. 已知




正确答案
解析

考查方向
解题思路
以集合A和集合B的交集是0为突破口,利用集合中元素的特征判断出m和n的值。
易错点
集合中元素的特征,忽略集合中的元素具有互异性
知识点
3. 若


正确答案
解析
因为
考查方向
解题思路
根据向量平行时数量积的特点进行求解
易错点
混淆向量平行和向量垂直时,向量数量积不同。
知识点
5. 已知数列


正确答案
解析
通过观察,可以看到,b2,b16和b9之间的关系,可以得到

考查方向
解题思路
利用等差中项求b9,进而求解答案
易错点
发现不到b2b16和b9之间的关系。
知识点
6. 一个锥体的正视图和左视图如下图,下面选项中,不可能是该锥体的俯视图的是
正确答案
解析
本题中给出了正视图与左视图,故可以根据正视图与俯视图长对正,左视图与俯视图宽相等来找出正确选项。A中的视图满足三视图的作法规则;B中的视图满足三视图的作法规则;C中的视图不满足三视图的作法规则中的宽相等,故其为错误选项;
D中的视图满足三视图的作法规则;
考查方向
解题思路
由三视图的作法规则,长对正,宽相等,四个选项进行对比,找出错误答案。
易错点
没有掌握住三视图的作法规则
知识点
7. 如果函数


正确答案
解析
因为图象关于点
φ=kπ-8×


考查方向
解题思路
先利用图象关于点对称求出φ的取值集合,然后求出最小值。
易错点
复合三角函数的对称性的应用
知识点
9. 已知




正确答案
解析
设g(x)=lnx,h(x)=1/x-1,在同一坐标中它们表示的图象如图所示,
要使f(x)=g(x)-h(x)=0,即g(x)=h(x),即它们相交,交点的横坐标就是零点。从图中可以看到,令x=a,时,g(a)>h(a),即f(a)>0,同理可得,f(b)<0,因此此题选C
考查方向
解题思路
此题用图像法解答
易错点
函数零点的概念理解不透彻
知识点
4. 已知P(B|A)= 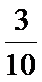
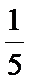
正确答案
解析
P(AB) = P(B|A) ·P(A)= 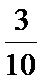
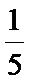
考查方向
解题思路
根据概率公式之间的转换公式计算
易错点
条件概率公式记混,不知道P(B|A)和P(A)的区别和联系
知识点
8.设点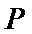
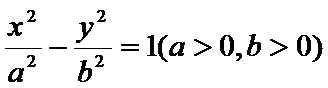
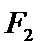
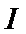
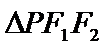
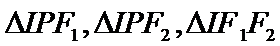
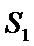
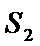
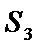
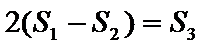
则双曲线的离心率为
正确答案
解析
由于I为△PF1F2的内心,故I到△PF1F2的三边距离相等,所以满足S1=S2+mS3,又因为2(S1-S2)=S3,所以m=2,且m就是此双曲线的离心率,所以选A.
考查方向
解题思路
根据双曲线的标准方程和定义,得到PF1-PF2=2a.
易错点
根据所给关系,找不到转化到双曲线离心率的突破口
知识点
10. 已知函数

正确答案
解析
根据分段函数求解集,根据图象可以判断,此题选C
考查方向
解题思路
首先画出y=f(x)和y=5的大致图象,然后判断解集
易错点
分段函数对应区间找不准
知识点
11. 直线








正确答案
解析
分别设A.B两点的坐标,分别带入抛物线与直线中,消去参数,得到点斜式方程,最后求得定点坐标(此题也可将选项带入验证得到答案)
考查方向
解题思路
将抛物线与直线联立,建立方程求得
易错点
计算能力
知识点
12. 正方体ABCD—A1B1C1D1的棱长为

条封闭的曲线,这条曲线的长度是
正确答案
解析
正方体的各个面根据与球心位置关系分为两类:ABCD、AA1DD1、AA1BB1为过球心的截面,截痕为大圆弧,各弧圆心角为60度,所以根据弧长公式可以求得
考查方向
解题思路
找到正方体的外接圆的圆心和半径,实际上是求球在正方体各个面上交线的长度计算。
易错点
空间想象能力和计算能力
知识点
13. 如图,在边长为1的正方形中随机撒1000粒豆子,有380粒落
到阴影部分,据此估计阴影部分的面积为 .
正确答案
0.18
解析
正方形的面积为1,设阴影部分的面积为S,因为随机撒1000粒豆子,有180粒落到阴影部分,所以几何概率公式进行估算:S:1=180:1000,即S=0.18,故答案为0.18
考查方向
解题思路
通过几何概率的意义计算
易错点
想不到是概率问题,用面积公式硬算
知识点
16.在













正确答案
解析
因为
且

因为


考查方向
解题思路
根据给出的向量之间的关系和线段之间的关系,利用余弦定理求解
易错点
向量模和向量平行概念不理解
知识点
14.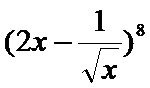
正确答案
1
解析
二次项系数和x的取值无关,所以令x=1,可以得到各项展开后和为1.
考查方向
解题思路
填空题可以选取特殊值
易错点
二项式展开后,逐一计算,繁琐容易出错
知识点
15.下列命题:①已知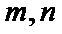
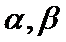
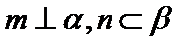
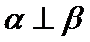
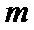
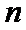
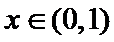
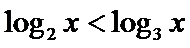
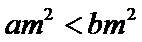
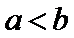
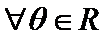
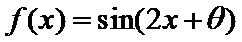
正确答案
①
解析
(1)正确(2)取x=1/2,则不等式不成立,(3)若m为0,则逆命题为假,忽略了等号,(4)当θ=π/2,时,函数为奇函数。所以答案填①
考查方向
解题思路
根据题意,逐个选项分析
易错点
相关知识点掌握不扎实
知识点
17.数列


(Ⅰ)求证数列
(Ⅱ)证明:对一切正整数

正确答案
见解析
解析
(1)由


所以
(2)由(1)知
又
故
考查方向
解题思路
利用构造的等比数列前n项和公式求解
易错点
构造等比数列
知识点
18.一个盒子里装有大小均匀的8个小球,, 其中有红色球4个, 编号分别为1, 2, 3, 4; 白色球4个, 编号分别为2, 3, 4,5. 从盒子中任取4个小球 (假设取到任何一个小球的可能性相同).
(Ⅰ) 求取出的4个小球中, 含有编号为4的小球的概率.
(Ⅱ) 在取出的4个小球中, 小球编号的最大值设为X, 求随机变量X的分布列.
正确答案
见解析
解析
(1)

X的分布列为
考查方向
解题思路
第一问将所有可能的情况列举出来求解,第二问根据随机变量分布列的概念及特征,一次写出当随机变量取不同值时的情况。
易错点
考虑情况不全面
知识点
19.边长为4的菱形





(Ⅰ) 求证:
(Ⅱ) 求二面角
正确答案
见解析
解析
(1)因为平面
则

(2)以


设
则

考查方向
解题思路
通过面面垂直证明线面垂直,找到二面角构造三角形,进而计算出二面角的平面角的正切值
易错点
找不到二面角
知识点
20.已知椭圆










(Ⅰ) 求弦
(Ⅱ) 若直线



正确答案
见解析
解析
(1)设


所以
(2)设


又
则
考查方向
解题思路
建立适当的坐标系,利用向量的数量积建立方程,进而求解。与椭圆联立成方程组,消元整理可得。
易错点
计算能力弱,
知识点
21. 已知函数

(Ⅰ)若

(Ⅱ)若对任意


(Ⅲ)设函数


正确答案
见解析
解析
解: 


则当



所以有
(2) 当




当



当





(3)


由此得,
故

考查方向
解题思路
确定f(x)的定义域,计算导数,求导函数等于0时的根,列表求解。
易错点
求导错误,构造函数,此题难度大
知识点
22.如图, 










(Ⅰ) 求证:
(Ⅱ) 若


正确答案
见解析
解析
(1)连结
因为


所以 
所以
由已知

所以

所以

(2) 因为
所以


所以
又因为


所以
所以 
考查方向
解题思路
利用辅助线,做出相似三角形,根据相似求出相关线段的长
易错点
辅助线,三角形相似条件找不准