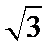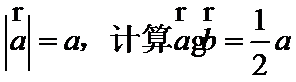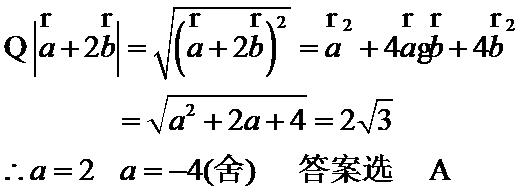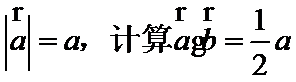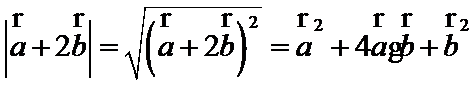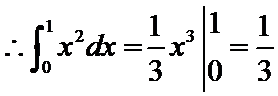- 真题试卷
- 模拟试卷
- 预测试卷
2.设集合

正确答案
解析
使用集合交集的性质,借助数轴容易得出答案。选A
考查方向
解题思路
本题属于简单题,可使用数轴表示出集合直接判断,
易错点
该题主要易错于对端点情况的判断错误
知识点
3.下列选项错误的是()
正确答案
解析
1、原命题与逆否命题的关系确定A正确
2、根据充分必要条件的判定确定B正确
3、根据全(特)称命题的否定确定C正确
4、最后选择D
考查方向
解题思路
1、原命题与逆否命题的关系确定A正确
2、根据充分必要条件的判定确定B正确
3、根据全(特)称命题的否定确定C正确
4、最后选择D
易错点
本题易错于全(特)称命题的否定理解不足,导致无法排除
知识点
6.在正项等比数列


正确答案
解析
考查方向
解题思路
本题属于基本概念题,使用直接法,
1、由题意得设
2、根据等比数列性质得出
3、使用等比数列的性质,比值转换为关于q的问题得出答案
易错点
该题出错在计算错误
知识点
8.三棱锥
正确答案
解析
根据三视图可知直观图为,如图可知
∴
考查方向
解题思路
1、根据三视图得到AC=4,点B到AC的距离以及垂足的位置判断,
2、根据直角三角形勾股定理直接算出结果
易错点
主要易错于三视图中长宽高的几何意义
知识点
9.如果执行如右面的程序框图,那么输出的S=()
正确答案
解析
考查方向
解题思路
1、写出循环结构,找出S结果的规律
2、找出程序框图解决的问题:求数列前n项和
3、找出跳出循环的位置即项数
易错点
本题易在判断上出错,导致提前或者延后跳出循环,第二没有发现S结果之间的规律,导致出错,
知识点
1.i是虚数单位,复数
正确答案
解析


考查方向
解题思路
本题属于简单题,可使用直接法,
(1)化简z得到
(2)观察实部和虚部对应的正负
易错点
计算过程易忽略
知识点
4.使函数


正确答案
解析
考查方向
解题思路
1、通过和角公式求函数y=Asin(

2、利用函数奇偶性以及在

3,根据选项得出结果
易错点
本题易于在求解
知识点
5.已知平面向量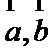
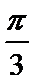
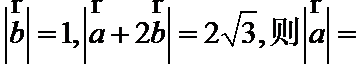
正确答案
解析
由题意得设
考查方向
解题思路
本题属于基本概念题,使用直接法,
1、由题意得设
2、根据数量积的性质
3、带入计算可得结果,注意a的范围
易错点
该题出错在计算错误
知识点
7.已知双曲线

正确答案
解析
利用抛物线的性质得出焦点为
所以双曲线方程为

考查方向
解题思路
1、利用抛物线的性质得出焦点为
2、根据双曲线的几何性质得出
3、根据双曲线的几何性质直接写出渐近线
易错点
本题主要易错于焦点位置的判断以及m的含义
知识点
10.某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声类节目的演出顺序,则同类节目不相邻的排法种数是()
正确答案
解析
解:分2步进行分析:1、先将三个歌舞类节目全排列,有
分2种情况讨论:
①将中间2个空位安排1个小品类节目和1个相声类节目,有
排好后,最后1个小品类节目放在2端,有2种情况,
此时同类节目不相邻的排法种数是
②将中间2个空位安排2个小品类节目,有
此时同类节目不相邻的排法种数是
则同类节目不相邻的排法种数是
故选B
考查方向
解题思路
根据题意,分2步进行分析:①,先将三个歌舞类节目全排列,②,因为三个歌舞类节目不能相邻,则分2种情况讨论中间2个空位安排情况,由分步计数原理计算没一步的情况数目,进而由分类计数原理计算可得答案.
易错点
本题易错于分类不清
知识点
11.函数

正确答案
解析
考查方向
解题思路
1、对每一段单独求解,但是要在取值范围以内
2、对解集取并集
易错点
本题易错于忽视前提条件
知识点
14.若


正确答案
解析
根据约束条件画出可行域
图可知
考查方向
解题思路
该题解题思路
1、题意画出可行域,标记可行域的定点
2、根据 
3、通过旋转移动得出最值
易错点
主要体现在两个方面①可行域不规范,②
知识点
12.二项式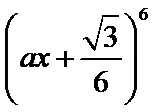
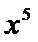
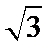
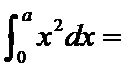
正确答案
解析
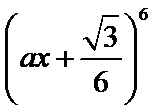
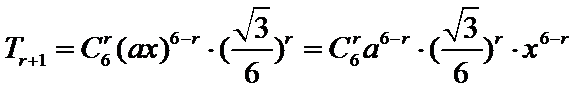
则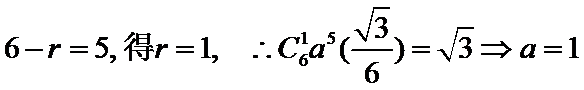
考查方向
解题思路
1、写出二项展开式,确定r,直接计算得到a,
2、根据定积分求出结果
易错点
本题易错在二项展开式记忆错误
知识点
13.锐角三角形ABC中,


正确答案
解析
利用正弦定理得出
又∵
考查方向
解题思路
该题解题思路如下1、利用正弦定理得出


易错点
该题易于忽略了对A的范围的判断,该题属于中档题
知识点
15.已知函数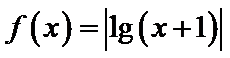
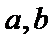
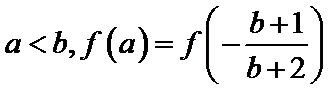
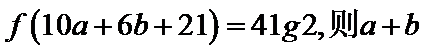
正确答案
考查方向
解题思路
该题解题思路
易错点
主要易错于函数中的绝对值不能去掉,不能判别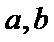
知识点
函数
16.求函数
17.若


正确答案
见解析
解析
考查方向
解题思路
该题解题思路如下利用数量积运算,得出
使用和角公式化简解析式成一角一函数,进而求出最大值
易错点
该题易于在角的范围上判断出错,
正确答案
见解析
解析
考查方向
解题思路
该题解题思路如下
根据正弦值和角的范围求余弦值
利用凑角的方式和两角和的余弦公式得到答案,
易错点
该题易于在角的范围上判断出错,



18.若平面


19.求平面
正确答案
见解析
解析
考查方向
解题思路
该题解题关键在于找到所求内容的突破点
确定线面平行判定的方式:线//面→线//线
由已知AD//BC,得到线//面
易错点
本题容易在辅助线建立过程出错,空间直角坐标系建立及其坐标表示出错,二面角的判断出错
正确答案
见解析
解析
考查方向
解题思路
该题解题关键在于找到所求内容的突破点
根据线//面→线//线
根据已知条件建立坐标系,并标记所需点的坐标
计算相应面的法向量,并求向量的夹角
判断两面角的大小确定二面角
易错点
本题容易在辅助线建立过程出错,空间直角坐标系建立及其坐标表示出错,二面角的判断出错
袋中共有8个球,其中有3个白球,5个黑球,这些球除颜色外完全相同.从袋中随机取出一球,如果取出白球,则把它放回袋中; 如果取出黑球,则该黑球不再放回,并且另补一个白球放入袋中.
20.重复上述过程2次后,求袋中有4个白球的概率;
21.重复上述过程3次后,记袋中白球的个数为X,求X的数学期望.
正确答案
见解析
解析
考查方向
解题思路
使用排列组合知识写出基本事件空间和4个白球个数(注意分类),并用古典概型的概率公式计算概率
易错点
本题易错在分类不清
正确答案
见解析
解析
考查方向
解题思路
分清X所有可能取值
根据情况依次求概率
写分布列以及期望
易错点
本题易错在分类不清
已知各项均不相等的等差数列



22.求数列


23.是否存在正整数

正确答案
见解析
解析
考查方向
解题思路
借助等差数列前4项和,与
解析式
易错点
本题易错于裂项等号不成立,第二问不理解题意
正确答案
见解析
解析
考查方向
解题思路
根据等比数列性质写出关系式
解不等式确定取值
易错点
本题易错于裂项等号不成立,第二问不理解题意
如图所示的封闭曲线C由曲线




24.求曲线
25.若点Q是曲线

26.若点F为曲线



正确答案
见解析
解析
考查方向
解题思路
根据离心率和点求出曲线
易错点
本题易错于1、曲线方程求错,特别是曲线
正确答案
见解析
解析
考查方向
解题思路
求出直线AB,判定面积最大是恰好是与AB平行且与曲线
易错点
本题易错于
1、曲线方程求错,特别是曲线
2、第二问Q点位置的确定,使用直接法会极大的增加运算过程,且很容易出错,第三问,主要是在圆的几何性质上使用出错
正确答案
见解析
解析
考查方向
解题思路
设出直线方程,利用与曲线

借助圆的几何性质
易错点
本题易错于1、曲线方程求错,特别是曲线
设函数
27.若

28.若

29.设

注:
正确答案
见解析
解析
考查方向
解题思路
借助导函数的正负直接求出单调区间
易错点
本题易错在第二问中的信息转化:函数

正确答案
见解析
解析
考查方向
解题思路
根据





易错点
本题易错在第二问中的信息转化:函数

正确答案
见解析
解析
考查方向
解题思路
本题解题思路
借助第二问的结论
易错点
本题易错在第二问中的信息转化:函数